An Optimal Analysis to the Prominent Iris Detail-Based Discrete Wavelet Transform to Reduce Fake Rejection Ratio
Department of Electronics and Communications Engineering, Technical Engineering College-Baghdad, Middle Technical University, Ministry of Higher Education & Scientific Research, Baghdad, Iraq
*Corresponding author. E-mail: alaakazzawi@mtu.edu.iq; ali_ksaleh2010@yahoo.com
Received: Mar. 10, 2022; Revised: Jun. 22, 2022; Accepted: Nov. 15, 2022; Published: Nov. 30, 2022
Citation: A.K. Al-azzawi. An optimal analysis to the prominent iris detail-based discrete Wavelet transform to reduce fake rejection ratio. Nano Biomedicine and Engineering, 2022, 14(3): 236–245.
DOI: 10.5101/nbe.v14i3.p236-245
Abstract
This paper presents a new technique by support vector machines after extracting the prominent iris features using discrete wavelet transformations, to achieve an optimal classification of energy system disturbances. A framework for iris recognition and protection of the recognition system from fake iris scenes was proposed. The scale-invariant feature transform is set as an algorithm to extract local features (key points) from iris images and their classification method. To elicit the prominent iris features, the test image is first pre-processed. This will facilitate confining and segmenting the region of interest hopefully, reducing the blurring and artifacts, especially those associated with the edges. The textural features can be exploited to partition irises into regions of interest in addition to providing necessary information in the spatial distribution of intensity levels in an iris neighborhood. Next, the detection efficiency of the proposed method is achieved through extracting iris gradients and edges in complex areas and in different orientations. Further, the iris diagonal edges were easily detected after calculating the variance of different blocks in an iris and the additive noise variance in a textured image. The vertical, horizontal, and diagonal iris image gradients with different directions were successfully extracted. These gradients were extracted after adjusting the threshold amplitude obtained from the histograms of these gradients. The average calculations of MAVs, peak signal-to noise ratios (PSNRs), and mean square errors (MSEs) within the orientation angles (‒45°, +45° and 90°) for both vertical and horizontal iris gradients had occurred within the rates of 1.9455–3.1266, 36.388–39.863 dB and 0.0001–0.0026, respectively.
Keywords: Support vector machines; Discrete wavelet transform; Feature selection technique;
Energy system disturbances; Scale-invariant feature transform; Artifacts
Introduction
Iris recognition is used as a reliable and distinctive identification card to a large extent and considered as an accurate biometric system. Iris is a large annular shape that is surrounded by a small annular shape, represented by the dark pupil. In the middle of a white sclera region, iris is used to provide an accurate interlacing properties as illustrated in Fig. 1. On the other hand, the iris may be unique in having different anatomical information from one person to another, which is almost stable throughout their life [1]. Most recognition systems use the following four stages: segmentation, iris acquisition, normalization and feature extraction, to provide an accurate personal identification. In addition, biometric system is itself a multi-disciplinary part of research that deals with artificial intelligence, image processing and computer vision. Here, the automated pattern recognition system extracts data necessary for individuals’ personal or physiological characteristics for the purpose of comparing them with the acquired database. One of the most important biometrics obstacles in the application of the iris recognition of an individual is in cases where the imaging in motion (the iris is at a distance and in motion) [2]. Therefore, the need to pay attention to the method of extracting the highlighted features which in turn may greatly facilitate the achievement of matching with the required pattern database. To overcome such problems, an additional analytical imaging innovator should be used, to provide more accurate recognition, and match the acquired database. This paper presents a solution strategy tested with individual noisy iris, by means of selective edge extraction procedures within complex regions (i.e., non-smoothed regions). Further, The high quality of the features extracted from iris can be achieved by using a support vector machine (SVM)-based enhancement algorithm [3]. To achieve an optimum extraction of iris feature vectors, both the Sobel operator and the local variance have been used in this paper. Here, SVM is used to classify the vectors of iris feature, which in turn provides adequate information about the point spread functions, as well as removing the noises.
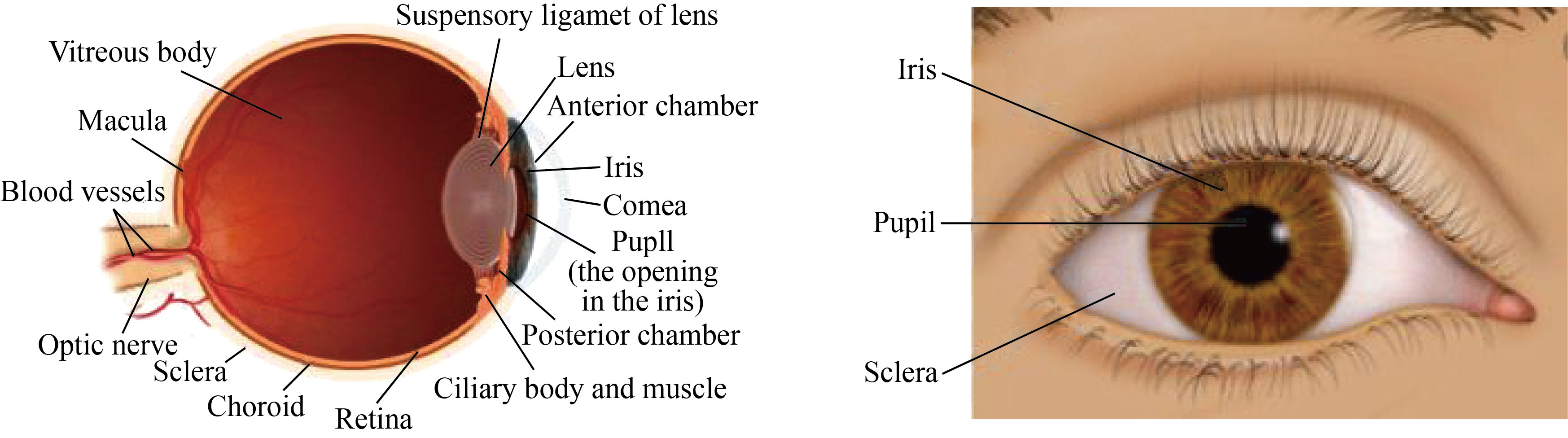
Fig. 1 Main parts of the human eye makeup
Iris recognition systems are considered highly confidential, due to the difficulty of cloning or dealing with the texture of iris [4]. Significantly, most contact lenses may impede the iris recognition systems from imaging the natural iris texture. Therefore, Iris’ commercial recognition systems must offer clear detection innovations when using contact lenses [5–7].
Recently, many innovative algorithms have provided many classifications of empirical combinations of iris image texture features. Further, a classifier is used in training these groups with the intention, to distinguish in which cases the texture lens was used or not [8, 9].
Therefore, our contributions lie in the following three aspects. First, create efficient training algorithms within an integrated secret system that detects colored texture lenses. These algorithms have the ability to penetrate this system and access personal data. These algorithms were based on the following three ratios: false acceptance ratio (FAR), false reject ratio (FRR) and correct classification rate (CCR). Second, exhibit an accurate segmentations in iris recognition regions through effective automated detection and for different types of colored texture lenses, which greatly improved the generalization. Third, use different sensors for the purpose of testing and checking the features of images acquired from texture lenses from different manufacturers. In this paper, an effective framework for detecting fake iris has been proposed. The scale-invariant feature transform (SIFT) is set as an algorithm to extract local features (key points) from iris images and their classification method.
The rest of this paper is organized as follows: Section 2 presents the wavelet-based energy features, and the vertical, horizontal and diagonal decomposition process. Brief reviews on iris fake detection and iris flash and movement detection process are proposed. The flowchart of an iris recognition system including iris fake detection is also given in this section. Section 3 presents the wavelet packet feature extraction.
The overall flowchart of the proposed method, the convolution process to the vertical and horizontal iris image gradients and several experimental results are illustrated and discussed in Section 4. Finally, Section 5 concludes the paper with suggestions for future work.
Wavelet-based Energy Features
Recently, the applications of wavelet analysis have become widespread in the field of research after the adoption of efficient analysis techniques. Wavelet analysis can be accomplished using several methods, including: short time Fourier transform (STFT), continuous wavelet transform (CWT), discrete wavelet transform (DWT) and discrete cosine transform (DCT).
In wavelet analysis, the test images can be decomposed at different sub-bands frequencies with different multi resolution time-frequency planes. On the other hand, wavelet analysis may help to reveal many meaningful aspects that other techniques may fail to detect such as trends and discontinuities. For a special set of filters g(n) and h(n), this structure is called the DWT, and the filters are called wavelet filters [10]. Figure 2 shows the process of decomposition of the “Haar” DWT. Here, DWT decomposes the image of the eye into four bands: LL (resolution), LH (vertical details), HL (horizontal details) and HH (diagonal direction details). The LL sub-band looks much closer to the original image, but its size is close to half the size of the original image through a down sampling process. Real time feature detection can be achieved when there is a trade-off between the adaptive speed of the controller and the detection accuracy of the wavelet filter. In general, the DWT is able to detect with high accuracy of the dynamic features of the scaling properties in the decomposed iris image. It is posible to successfully merge them into a multiple fractal formalism.
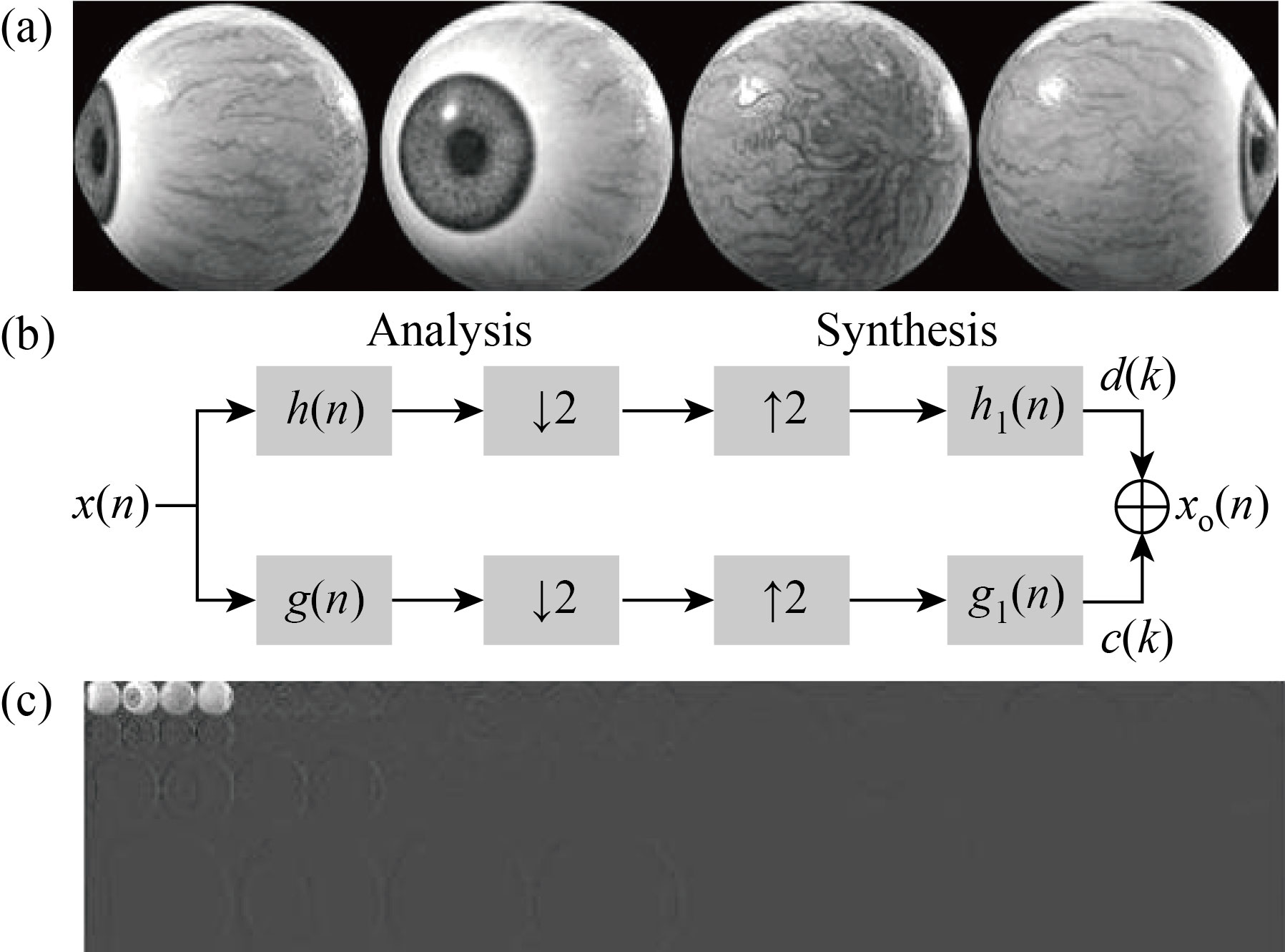
Fig. 2 Decomposition process: (a) gray-scale image, (b) wavelet filters and (c) 3-levels DWT decomposition
Figure 3 was presented in this paper as a test model for detecting the gradients and edges of the iris within different guiding angles.
Fig. 3 Test image presented in detecting the inclinations and edges of the iris at different guiding angles
Referring to Fig. 2, the synthesis filters are analogous to the analysis filters. But the filtering processes for synthesis the iris image are produced by convolutions rather than correlations for analysis. The discrete expansion coefficient sequence, c(k) and d(k), can be calculated by
![]() (1)
(1)
![]() (2)
(2)
These are the correlation among the iris data co, g(n) and h(n), respectively. This is followed by down sampled by a factor of two, because of the double-shift of g(n) and h(n) in the correlations. The discrete inter scale coefficients g(n) and h(n) are called the discrete low-pass and high-pass filters, respectively. The zero crossing information of the wavelet transformations may correspond to the edges in the iris form which can be derived from the wavelet detail sub-bands. On the other hand, this information can be distinguished as an accurate texture after changing the length scales. Figure 4 shows the vertical, horizontal and diagonal decomposition processes of the iris image using 3-level “Haar” decomposition.
Here, the feature vector represented by a homogeneous iris texture image can be classified after using a symmetric wavelet filters to reduce the associated distortion effects (i.e., blurring and artifact). The above texture classification can be improved by using fewer “Haar” decomposition-levels of the iris image, to achieve larger vector lengths.
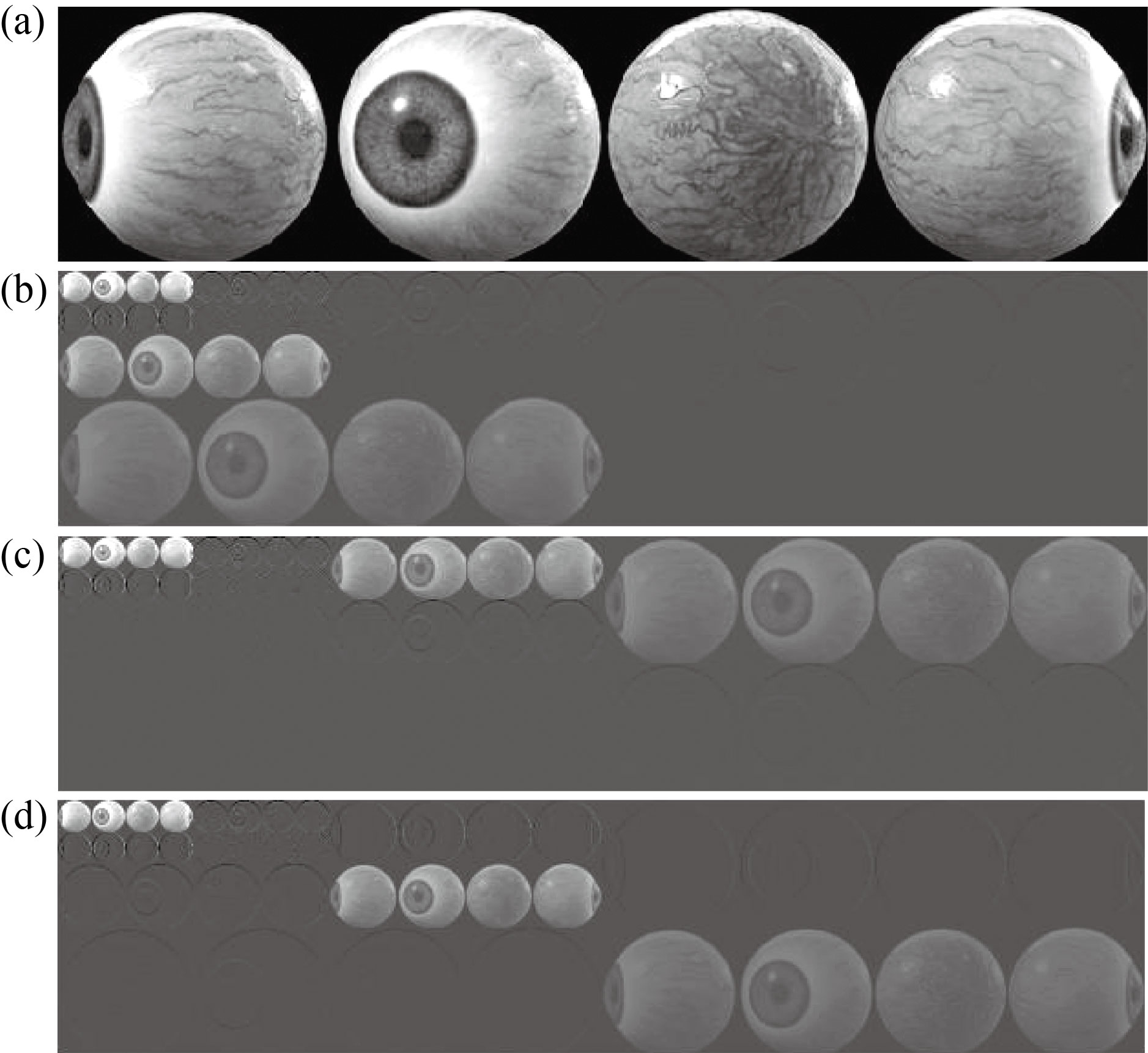
Fig. 4 3-level “Haar” DWT: (a) gray-scale-image, (b) vertical decomposition, (c) horizontal decomposition, and (d) diagonal decomposition
Iris Fake Detection
Most of the researches presented within the recognition areas for different irises were limited only to matching between storage data and test patterns. The challenge requires extensive study by creating smart security algorithms that support templates and make them an encrypted and more confidential database. Therefore, efficient detection is required to distinguish fake iris images from others (i.e., digital images). The authors in Refs. [11, 12] had presented an investigational study on the effect of the use of contact lenses as a detection method for fake images on the iris recognition system for detecting the features of statistical images.
In this paper, an effective framework that presents the textured and structured content of the iris has been proposed, as well as protecting the recognition system from the fake iris. The contributions of the paper are summarized in the following three points:
(1) A Gaussian blurring technique to reducing the noise in an iris test image is used. This is for the purpose of achieving active detection of the highlighted features of the iris image, which are not dependent on a scale while eliminating any noise.
(2) Blur iris images for multiple scales were created. Creating a new set of iris images with different scales, this would have required us to halving the scale. Further, the features extracted from iris have been enhanced with the use of different Gaussian techniques (feature enhancement algorithm).
(3) An SVM classifier for fake iris detection is proposed. This classifier, after continuous training, checks the recognition of the iris and compares the highlighting features detected with the storage templates.
Figure 5 presents our proposed framework for iris recognition and protection of the recognition system from fake iris scenes. SIFT was set as an algorithm that extracts the local features in the digital iris images and their classification method. SVM is one of the most popular classifiers used as a discriminant analysis to find a hyper-plane.
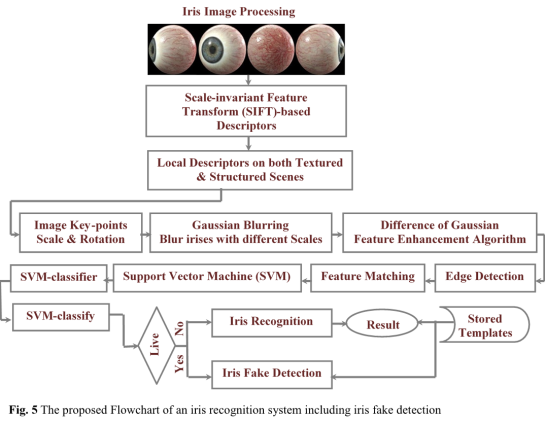
Fig. 5 Proposed flowchart of an iris recognition system including iris fake detection
It maps the data I in the input space L into a high dimensional space H (I![]() RL
RL![]() Φ(I)
Φ(I)![]() RH) mathematical kernel function Φ(I) to find the searching hyper-plane. The local features extracted from the test iris are commonly known as the key-points of the iris image. These key-points are scale and orientation invariants used in iris matching process. Further, one of the main advantages of the SIFT features is that they are not affected by the size and orientation of the iris image. Conversely, it requires us to distinguish the highlighted features while attenuating any noise, as well as ensuring that the extracted features are not dependent on the iris image scale. A Gaussian blurring technique has been adopted to reduce the noise in the iris image, hopefully, searching for the highlighted features on multiple scales.
RH) mathematical kernel function Φ(I) to find the searching hyper-plane. The local features extracted from the test iris are commonly known as the key-points of the iris image. These key-points are scale and orientation invariants used in iris matching process. Further, one of the main advantages of the SIFT features is that they are not affected by the size and orientation of the iris image. Conversely, it requires us to distinguish the highlighted features while attenuating any noise, as well as ensuring that the extracted features are not dependent on the iris image scale. A Gaussian blurring technique has been adopted to reduce the noise in the iris image, hopefully, searching for the highlighted features on multiple scales.
In addition, a difference of Gaussian was used as a method to enhance the extracted highlighted features, after the process of subtracting one version of the blurred iris image from another version with less blurring.
In practice, a radial kernel function (RKF) was adopted in extracting the highlighted iris features with different scale deviations (σ):
![]() (3)
(3)
where Ii is the highlighted input features.
To improve detection performance and make it more confidential and reliable, the paper introduces an intelligent detection algorithm, which tracks natural eye movements in different directions. This is almost unavailable in fake images. Figure 6 presents an accurate segmentation as part of the robust detection of iris features, within natural eye movements and in different directions.
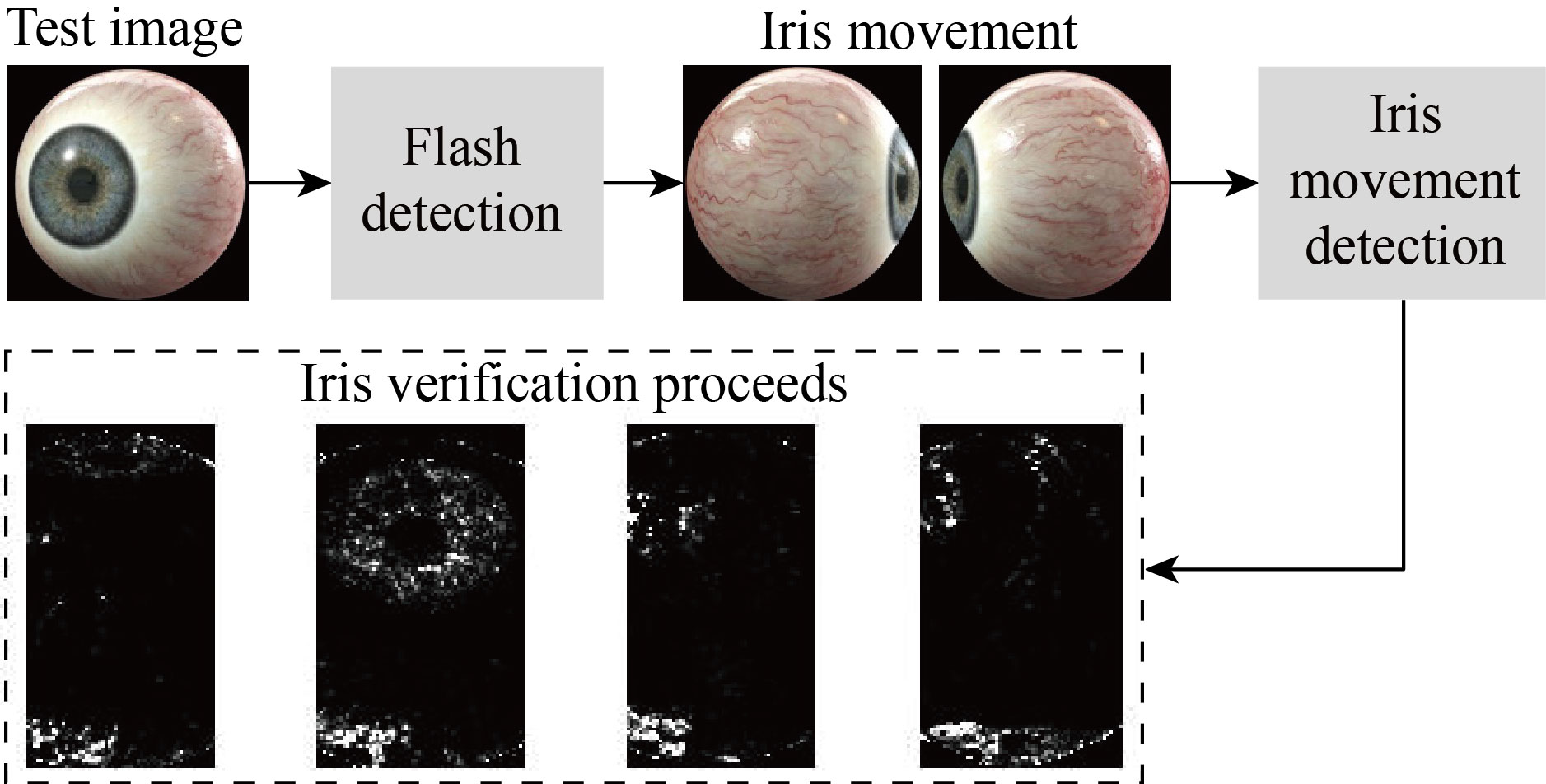
Fig. 6 Iris flash and movement detection process
Wavelet Packet Feature Extraction
The DWT is considered as the necessary tool in classifying and extracting the highlighting features of iris images, because of its ability to parenthesizing textures with a high resolution, scale invariant representation and in an elegant manner. This feature will greatly facilitate the process of extracting the necessary gradients and edges within the complex regions of the iris (i.e., smooth regions). In this paper, the features of scale and orientation were adopted in distinguishing textures extracted from wavelet coefficients, and then identifying the exact details of that texture. Further, the DWT inherently is a shift invariant tools, which might make the extracted texture shift invariant too. So, a multi scale shift-invariant DWT (SIDWT) is used to ensure extracting invariant features. The application was implemented over all sub-bands and in predetermined directions, to extract the largest possible number of texture features.
The optimal method for extracting the features of the essential content of iris images is still a challenge for many researchers in this field. In this paper, the focus is on the latest advanced techniques exploited in extracting the prominent local features after accurate detection of the iris content. To achieve an optimal wavelet analysis, “Haar” decomposition was adopted to decompose the detail and approximation of the iris coefficients at each of the three decomposition levels.
The mean absolute value (MAV) on N iris samples was adopted and given via
![]() (4)
(4)
where In is the n-th sample of the iris wavelet coefficients. Further, the scale-average wavelet power (SAP) is also evaluated to examine the fluctuations in power over a range of particular scales:
![]() (5)
(5)
where IWCs are the iris wavelet coefficients, M is the scale size, and n is the time parameter. The energy of a PWT iris coefficient (IWCs) at level j and time k is given by
![]() (6)
(6)
While the entropy can be determined using the extracted iris PWCs:
![]() (7)
(7)
Furthermore, the mean absolute error (MAE) values between the estimated iris image gradients vectors EV and the original iris image gradients vectors OV can be determined via
![]() (8)
(8)
where K is the vector dimension, N is the number of the input vectors in the test, EV is the estimated iris image gradients vector, and OV is the original iris image gradients vector. The performance efficiency in predicting iris image gradient vectors was evaluated by adopting the calculation of PSNR and given by
![]() (9)
(9)
Experimental Results and Discussion
The clearest borders images, the essential binary with filled holes and the essential binary and digital iris gradients were smoothly extracted. These gradients were one of the basic necessities in achieving the requirements of extracting the highlighted features from iris images, as shown in Fig. 7.
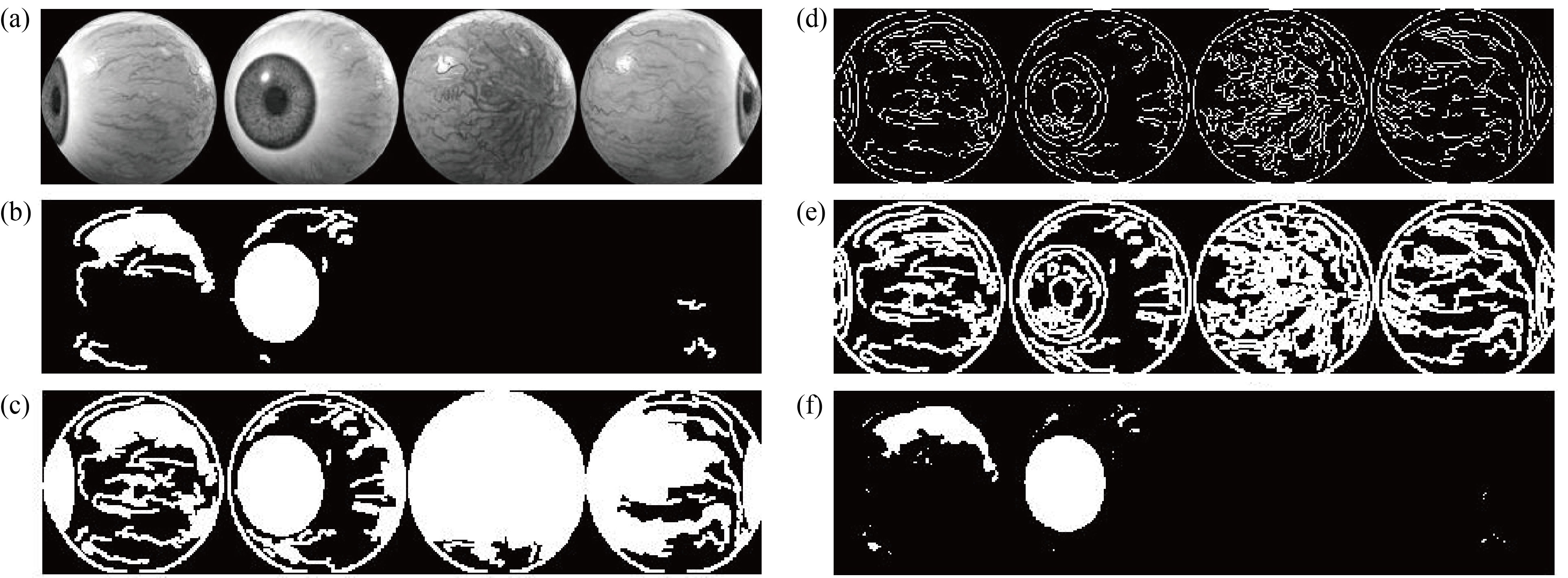
Fig. 7 Features extraction: (a) original image, (b) cleared border image, (c) essential binary with filled holes, (d) essential binary gradients, (e) essential digital gradients, and (f) more cleared border image
Figure 8 shows the proposed scheme for extracting potential gradients and edges in the test image. Our proposed method relied on the discrete cosine transform (DCT) coefficients to extract the vertical, horizontal, and diagonal edges in the sub-blocks of the test image. Image gradient is a directional variation in the intensity in an image. Generally, image gradients are used to extract information, robust feature and texture matching, and detect important edges from images, enabling us to locate the outlines of objects in the images. This may contribute to determining the highlighted details of the images by extracting the histograms of the image gradient vectors. Image gradients are usually extracted by convolving with a simplest filter such as Sobel operator or Prewitt operator. At a given orientation, the intensity of the gradient image is compared with that of the original image to get the final direction range. After calculating the gradients of prominent images, it is therefore necessary to consider the pixels with the largest gradient values in the direction of the gradient as possible edge pixels. In this context, a threshold should be extracted from the histogram of the image gradient magnitudes. This may make it easier to extract the largest number of edges after varying the angles of the vector, which in turn is used to search the image gradients and by varying the magnitude of the threshold.
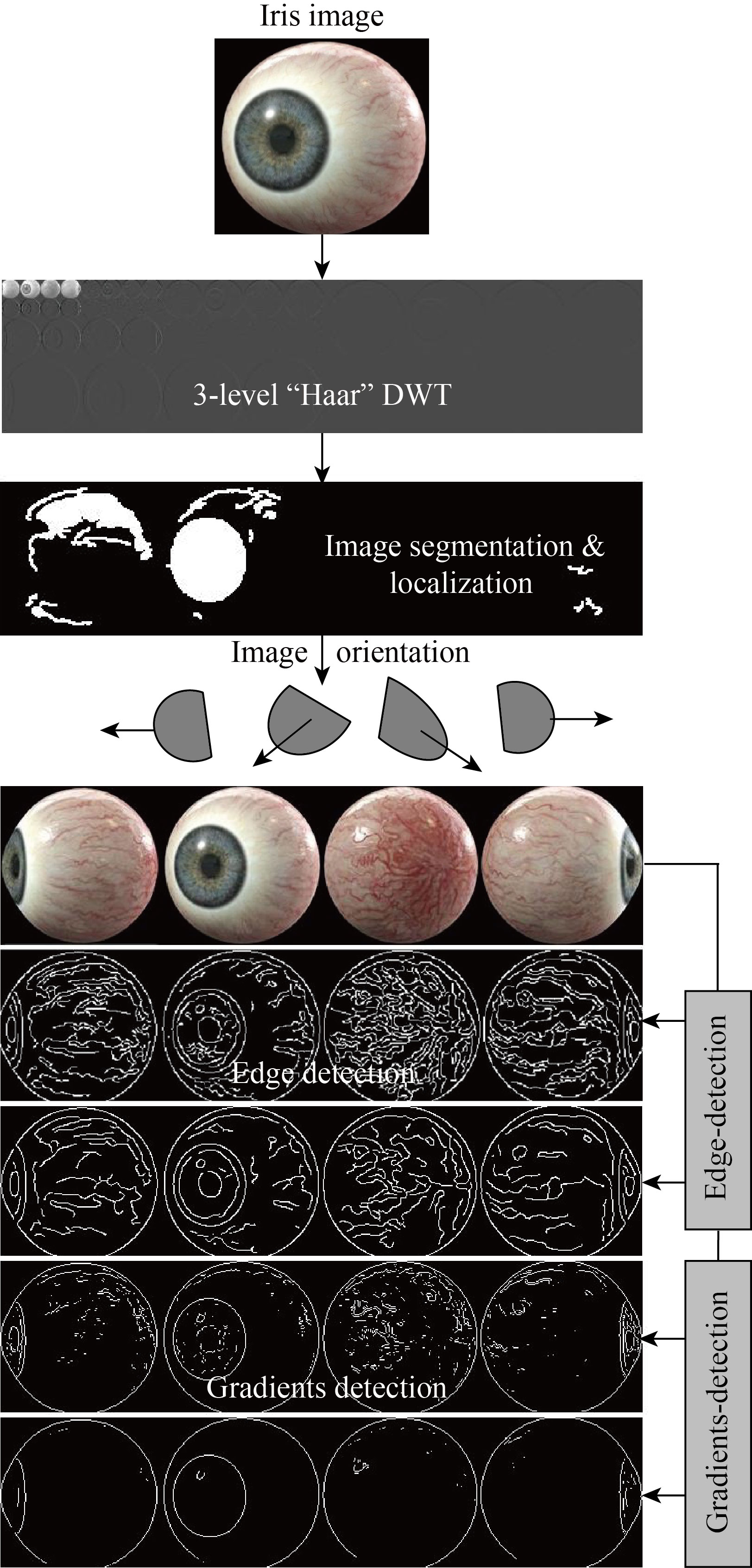
Fig. 8 Overall flowchart of the proposed method
The calculation of energy, entropy, MAVs and PSNR & MSEs for both vertical and horizontal iris image gradients has been shown in Table 1.
Table 1 Calculation of energy, entropy, MAVs and PSNR & MSEs for both vertical and horizontal iris gradients
|
|
|
|
|
| 897322.1256 | 895779.0145 | 985744.1256 | 1528935.00346 |
| -32568.18895 | -32676.01156 | -38652.23478 | -46459.03433 |
| 3.1266 | 2.3267 | 2.1469 | 1.9455 |
| 36.388 | 38.792 | 39.464 | 39.863 |
| 38.277 | 38.688 | 39.371 | 39.762 |
| 0.0026 | 0.0020 | 0.0007 | 0.0005 |
| 0.0018 | 0.0012 | 0.0005 | 0.0001 |
On the other hand, extracting the gradients and edges of the iris test images of our proposed method within the smooth and non-smooth areas was accomplished with high accuracy Extracting the edges from the iris images is one of the necessary steps in verifying the physical test content of the highlighted features within the detection region. In this paper, extracting edges were based on the evaluation of the partial derivative in both i and j directions, and predefined as Si and Sj, respectively. Ensuring strong edges lies in extracting both the vertical and horizontal gradients and histograms of the iris image. The gradients in both i and j directions can be evaluated by adopting
![]() (10)
(10)
where VG(i, j) are the vertical iris gradients and HG(i, j) are the horizontal iris gradients, respectively. A 3×3 row/column masks were used for the purpose of performing the convolution process between the pixels represented by the gradients with high magnitudes with those masks. These gradients were calculated via
![]() (11)
(11)
![]() (12)
(12)
where PS(i, j) are the strong pixels with high amplitudes iris gradients, MV(i, j) is a 3×3 row/column selected vertical mask and MH(i, j) is a 3×3 row/column selected horizontal mask. On the other hand, both the amplitude and orientation of these gradients were expressed by adopting the following two directional derivations ∂V(i, j) and ∂H(i, j). Here the amplitude and orientation of these gradients are given via [13]
![]() 1/2 (13)
1/2 (13)
where |![]() AIG| is the absolute amplitude of vertical and horizontal iris image gradients.
AIG| is the absolute amplitude of vertical and horizontal iris image gradients.
![]() (14)
(14)
Figure 9 presents our convolution process to the vertical and horizontal iris image gradients. The letters (A, B, C, D, E, F, G, H, and I) correspond to the I, and j vectors are (i–1, j–1), (i–1, j), (i–1, j+1), (I, j–1), (I, j), (I, j+1), (i+1, j–1), (i+1, j) and (i+1, j+1), respectively. A best match between E and the top pixels, (A, B and C) is achieved after assessing that the boundary matches
with the mean absolute difference (MAD).
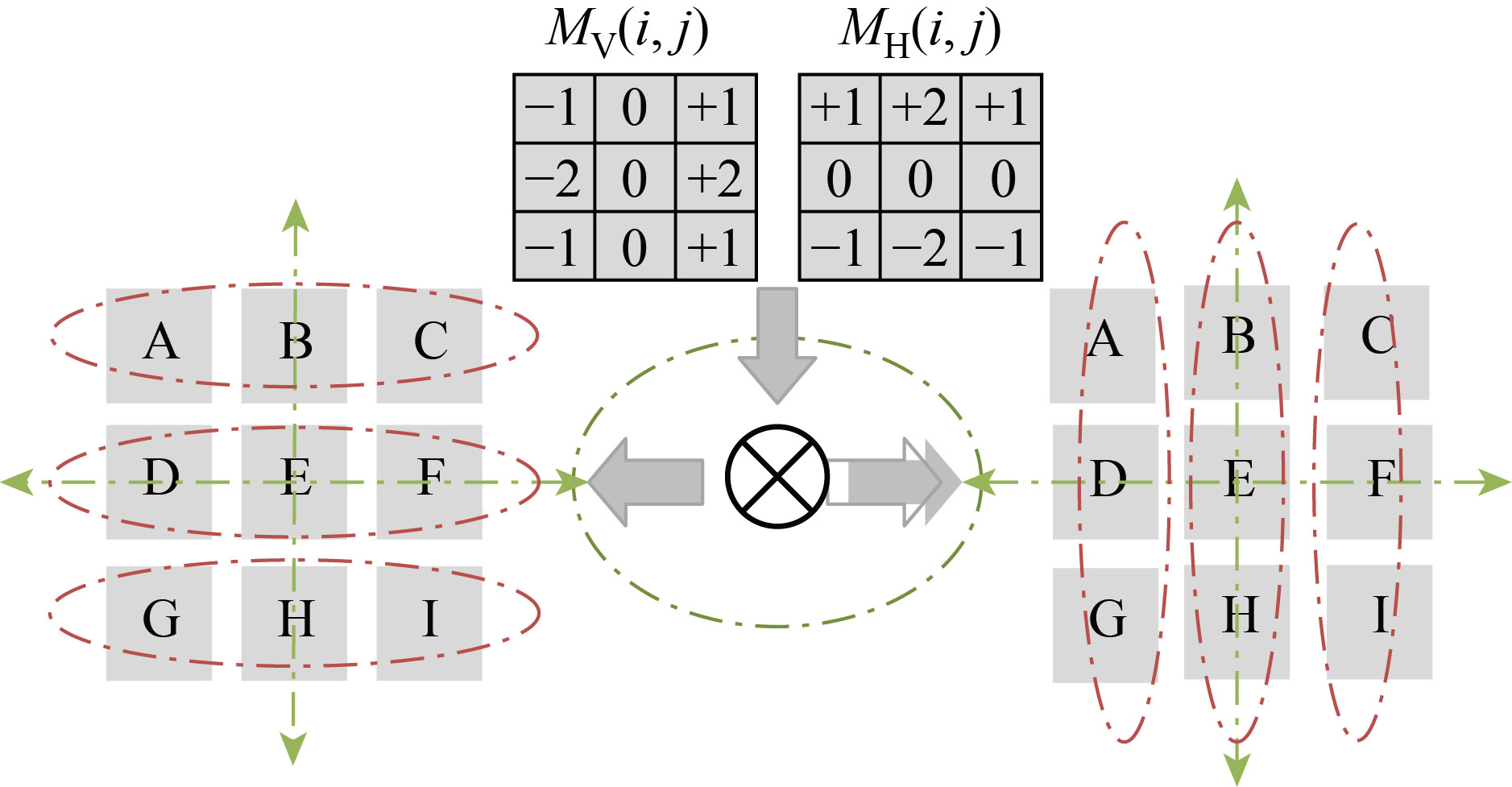
Fig. 9 Convolution process to the vertical and horizontal iris image gradients
![]() (15)
(15)
where SV is a search vector that is from –M to M. If the block size is M×M then E is the bottom block, and A, B, and C are the top left, top center, and top right, respectively. The best match algorithm (BMA) with respect to the minimum MAD is evaluated via [14]
![]() ] (16)
] (16)
So, in the case where the edge direction is between ![]() and
and ![]() , then the best match is found between pixel B and pixel C.
, then the best match is found between pixel B and pixel C.
Whereas, in the case where the edge direction is between 90° and 135°, the best match will lie between pixel A and pixel B. As a result, when the result of BMA is less than the threshold level, this indicates the appearance of meaningful edges or the appearance of pixels within a smooth area. Furthermore, a low-pass wiener filtering (LWF) is utilized for filtering the gray-scale iris image to preserve the edges and other high-frequency parts of iris image. The novelty of our proposed filter lies in employing an additive mean filtration rate for all pixels located in the vicinity of the processed pixels hopefully, to attenuate the noise and artifacts. Figure 10 presents the meaningful iris gradients.
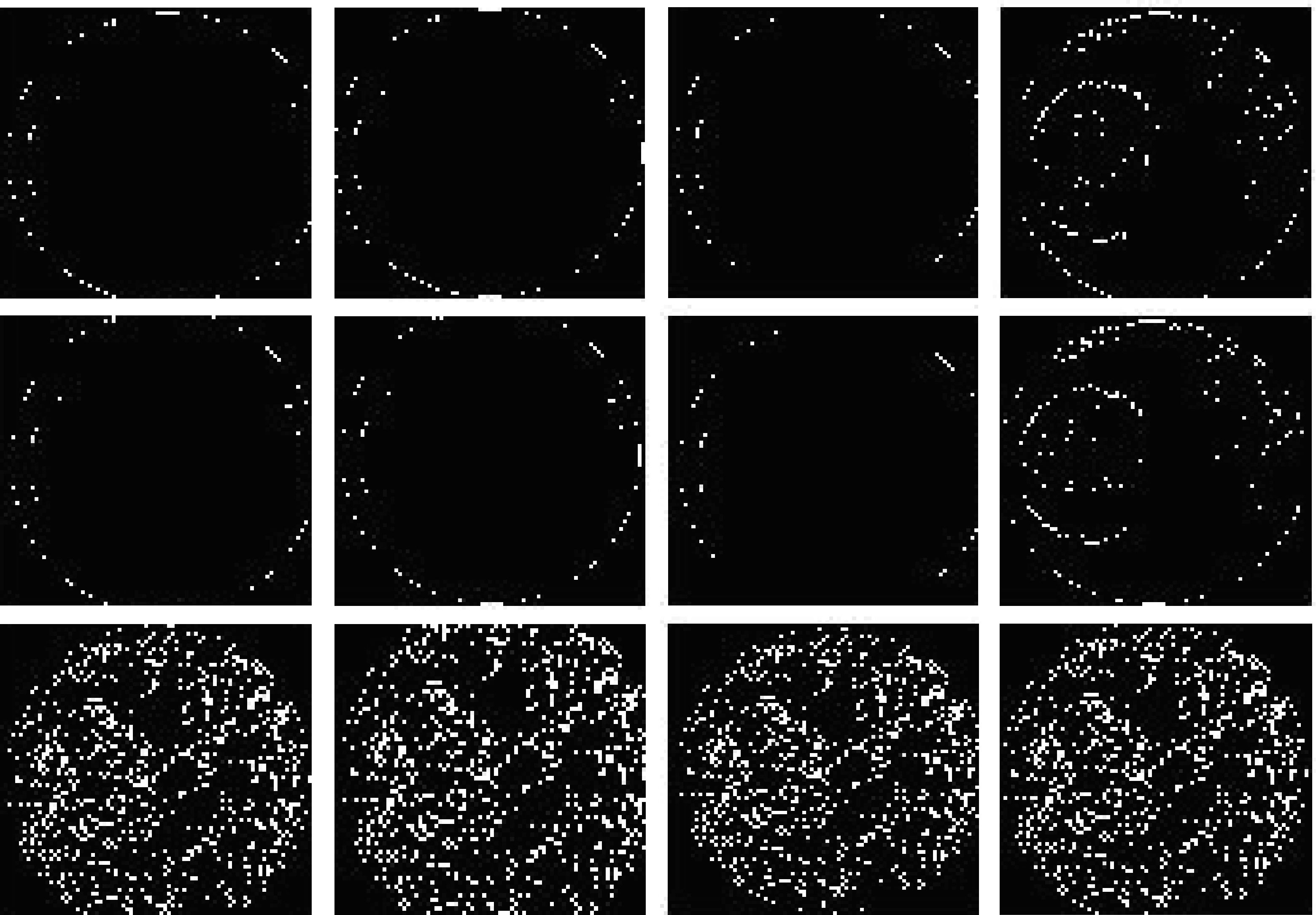
Fig. 10 Meaningful iris image gradients within smoothing areas
The final detection results for the gradients and edges located within the interest detection areas are represented by the cleared border features, which were previously detected in Fig. 7, as shown in Fig. 11. Whereas the PSNRs versus MSEs simulation sketches are shown in Fig. 12. For clarity, the gradients and edges of the iris are extracted from the areas of interest with different orientation angles to ensure that the maximum number of these gradients was extracted. These results can be exploited as a reference for comparison or as a reliable database in comparison with other iris data.
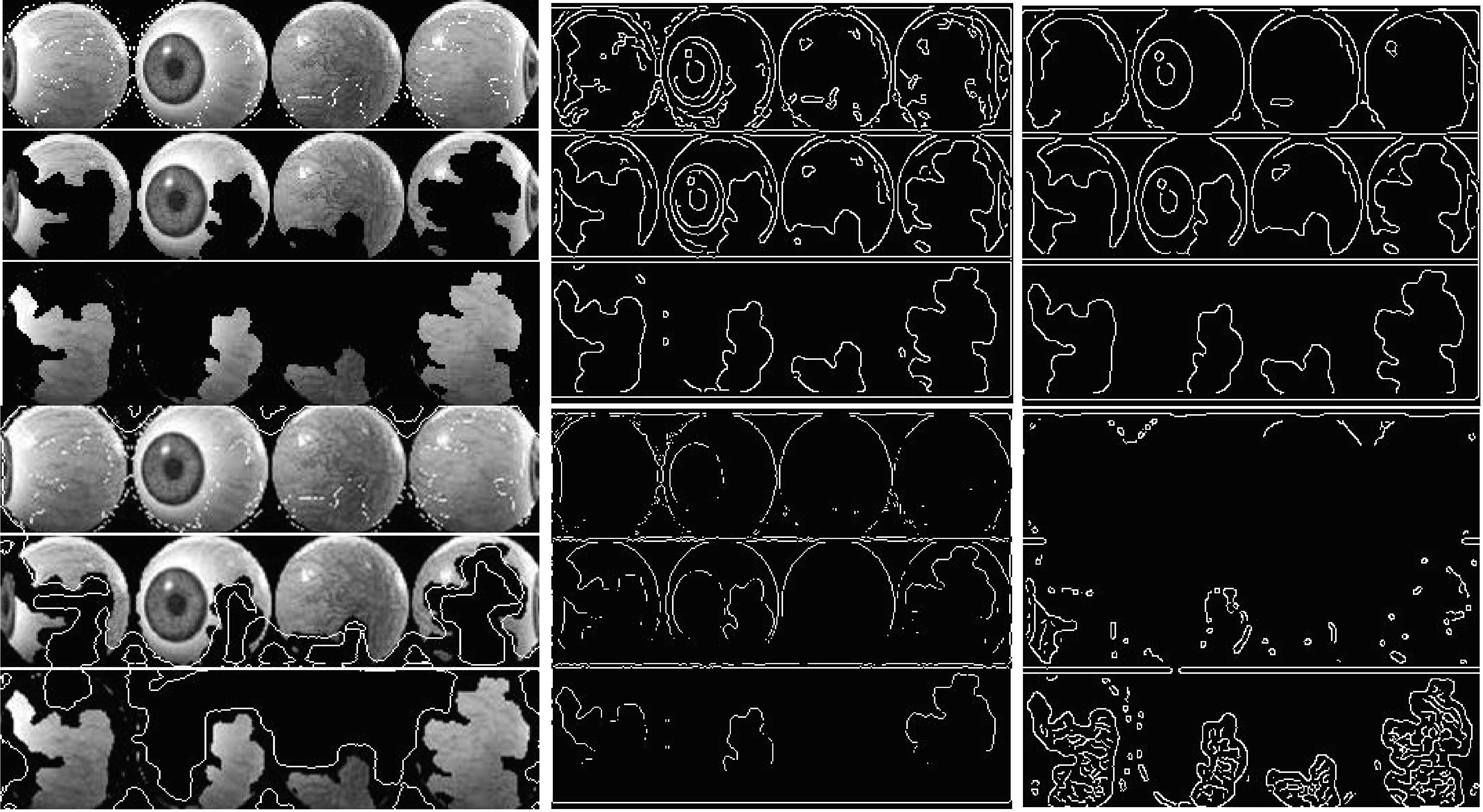
Fig. 11 Final detection results for the edges and gradients of the iris located within the detection areas of interest and extracted from the cleared border which were previously detected
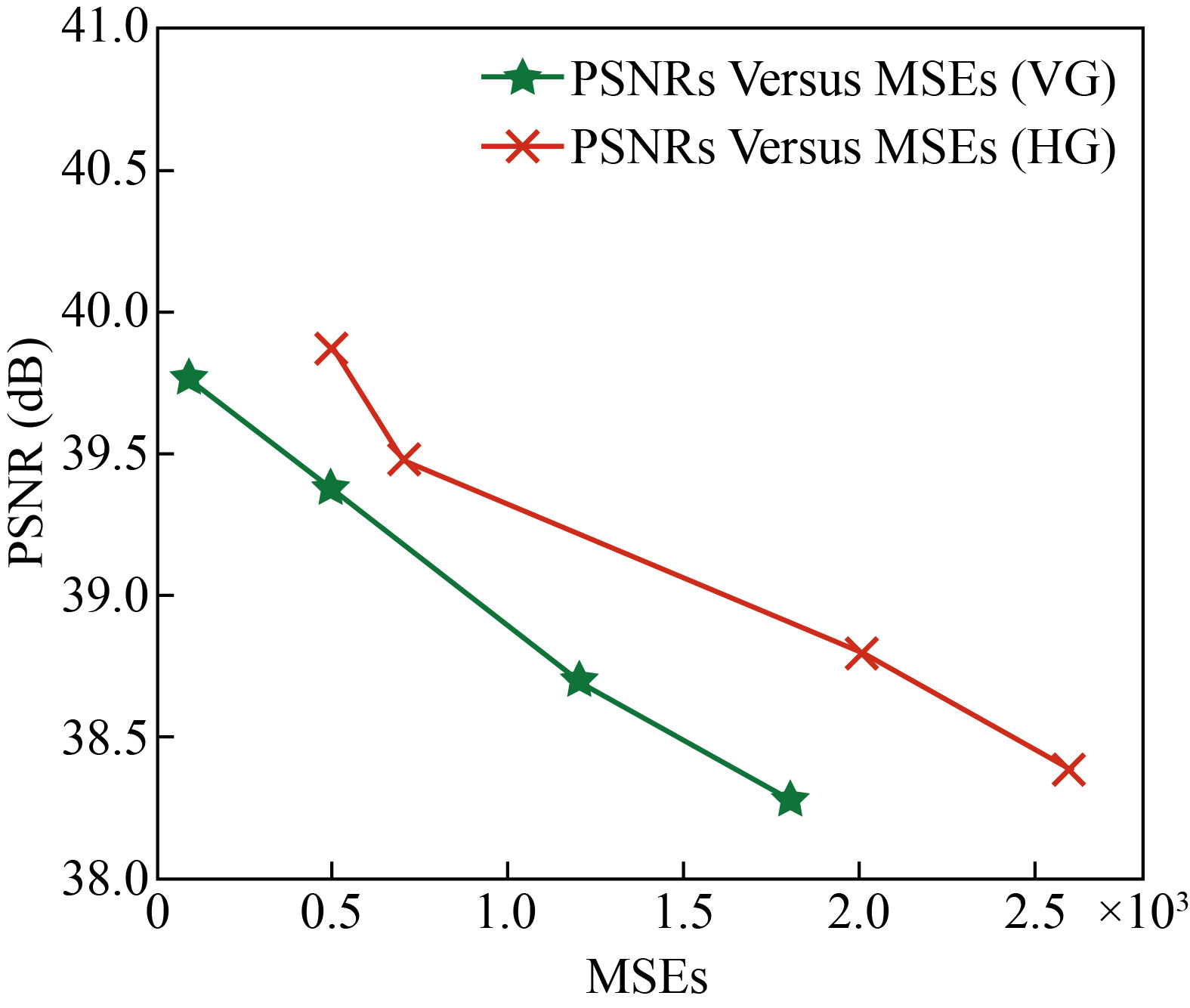
Fig. 12 PSNRs versus MSEs simulation sketches
Conclusion
Extraction of the prominent iris features was done very efficiently by using DWT as a supporting method for SVMs to show an optimal classification in energy system disturbances. In a sequential manner and by adopting five successive stages, the most prominent details of the iris were extracted within the predetermined detection areas. Initially, the test image was pre-processed to facilitate segmentation of the region of interest hopefully, reducing the blurring and artifacts, especially those associated with the edges. Subsequently, textural features were used as a method to identify areas of interest, as well as providing valuable information within the spatial distribution of the varying levels of density in an iris neighborhood. A low-pass wiener filtering (LPWF) was used to filter the gray-scale iris image in the intention, preserving the edges and other high frequency parts of iris image. The goal behind using this filter is to achieve an average additive filtration rate for all pixels located in the vicinity of the processed pixels hopefully, to attenuate the noise. Further, the vertical and horizontal iris gradients and edges within the complex regions (smooth regions) were extracted efficiently with different directions. These gradients were extracted after adjusting the threshold amplitude obtained from the histograms of these gradients. Furthermore, the diagonal edges are also easily extracted, after calculating the variance of different blocks and the additive noise variance within the target area. The experimental results of the proposed method had classified the detection areas in a flexible and robust manner. The simulation results were fairly accurate compared with other traditional literature methods, especially within the complex detection regions (smooth regions). The average calculations of MAVs, PSNRs and MSEs within the orientation angles (–45°, +45° and 90°) for both vertical and horizontal iris gradients had occurred within the rates of 1.9455–3.1266, 36.388–39.863 dB and 0.0001–0.0026, respectively.
Conflict of Interests
The authors declare that no competing interest exists.
Reference
[1] J. Kim, S. Cho, J. Choi, et al. Iris recognition using wavelet features. Journal of VLSI Signal Processing Systems for Signal, Image, and Video Technology, 2004, 38(2): 147–156. http://dx.doi.org/10.1023/B:VLSI.0000040426.72253.b1
[2] R. Szewczyk, K. Grabowski, M. Napieralska, et al. A reliable iris recognition algorithm based on reverse biorthogonal wavelet transform. Pattern Recognition Letters, 2012, 33(8): 1019–1026. http://dx.doi.org/10.1016/j.patrec.2011.08.018
[3] N. Nguyen, P. Milanfar, G. Golub. Efficient generalized cross-validation with applications to parametric image restoration and resolution enhancement. IEEE Transactions on Image Processing, 2001, 10(9): 1299- 1308. http://dx.doi.org/10.1109/83.941854
[4] A.K. Jain, A. Ross, S. Prabhakar. An introduction to biometric recognition. IEEE Transactions on Circuits and Systems for Video Technology, 2004, 14 (1): 4-20. https://doi.org/10.1109/TCSVT.2003.818349
[5] P. Mlyniuk, J. Stachura, A. Jiménez-Villar, et al. Changes in the geometry of modern daily disposable soft contact lenses during wear. Scientific Reports, 2021, 11: 12460. https://doi.org/10.1038/s41598-021-91779-y
[6] Ş. Ţălu, M. Ţălu, S. Giovanzana, et al. A brief history of contact lenses. Human and Veterinary Medicine, 2011, 3(1): 33-37. http://www.hvm.bioflux.com.ro/ docs/2011.3.33-37.pdf
[7] H. Wagner. The how and why of contact lens deposits. Review of Cornea & Contact Lenses, 2020, MAY/ JUNE: 30–37. https://www.reviewofcontactlenses.com/CMSDocuments/2020/05/MayJune2020RCCL.pdf
[8] V. Ruiz-Albacete, P. Tome-Gonzalez, F. Alonso Fernandez, et al. Direct attacks using fake images in iris verification. Biometrics and Identity Management, 2008: 181–190. https://doi.org/10.1007/978-3-540-89991-4_19
[9] D. Yadav, N. Kohli, J.S. Doyle, et al. Unraveling the effect of textured contact lenses on Iris recognition. IEEE Transactions on Information Forensics and Security, 2014, 9(5): 851–862. http://dx.doi.org/10.1109/TIFS.2014.2313025
[10] I. M. Dremin. Wavelets: Mathematics and applications. Physics of Atomic Nuclei, 2005, 68: 508–520. https://doi.org/10.1134/1.1891202
[11] D. Yadav, N. Kohli, J.S. Doyle, et al. Unraveling the effect of textured contact lenses on Iris recognition. IEEE Transactions on Information Forensics and Security, 2014, 9(5): 851–862. http://dx.doi.org/10.1109/TIFS.2014.2313025
[12] J.S. Doyle, K.W. Bowyer. Robust detection of textured contact lenses in Iris recognition using BSIF. IEEE Access, 2015, 3: 1672-1683. http://dx.doi.org/10.1109/ACCESS.2015.2477470
[13] A.K. Al-Azzawi, M.I. Saripan, A. Jantan, et al. A review of wave-net identical learning & filling-in in a decomposition space of (JPG-JPEG) sampled images. Artificial Intelligence Review, 2010, 34: 309–342. http://dx.doi.org/10.1007/s10462-010-9177-7
[14] A.K. Al-Azzawi, R.W.O.K. Rahmat. Wavelet neural network for vector prediction to fill-In missing image blocks in wireless transmission. Arabian Journal for Science and Engineering, 2013, 38: 3309–3320. http://dx.doi.org/10.1007/s13369-013-0666-2
Copyright© Alaa K. Al-azzawi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.