QDs-Cavity Approach to Controlled Quantum Teleportation of GHZ-Like State

 

Kexiang Hu 1 ,Baiqi Jin 2*, Qingkang Wang 1*

 

1 Key Laboratory for Thin Film and Microfabrication Technology of Ministry of Education, National Key Laboratory of Micro /Nano Fabrication Technology, Research Institute of Micro/Nano Science and Technology, Shanghai Jiao Tong University, Shanghai, 200030, P. R. China.

2 C.N. Yang Institute for Theoretical Physics, State University of New York at Stony Brook, NY 11794, USA College of Physics and Electronic Information, Wenzhou University, Wenzhou 325035, P.R. China.

 

* Corresponding authors. E-mail: wangqingkang@sjtu.edu.cn; americahuanyu@163.com; k.-x.hu@163.com

 

Citation: K. Hu. et al., QDs-Cavity Approach to Controlled Quantum Teleportation of GHZ-like State. Nano Biomed. Eng., 2010, 2(2): 109-116.

DOI: 10.5101/nbe.v2i2.p109-116

 

Abstract

The experimental scheme for controlled quantum teleportation of tripartite GHZ-like state is presented. With the entanglementgenerating through the interaction between the quantum dots in microcavities and a single photon, the controlled teleportation can be realized by virtue of Faraday rotation, single photon detection and electron spin orientation measurement. The success probability of the scheme can reach 1 if the cavities are switchable to choice the appropriate Faraday rotation angle. The scheme can be easily generalized to the teleportation of multipartite GHZ-like state.

 

Keywords: Controlled quantum teleportation; QDs-cavity system; Faraday rotation; Multipartite GHZ-like state

 

1. Introduction

Quantum information physics has developed into anextensive field involving the subjects of physics, informatics,  computer, engineering  science,  chemistry and mathematics etc. and the corresponding researchwork of the past several years has greatly clarified boththe theoretical potential and the experimental challenges of quantum information physics.To produce working laboratory devices that perform this profoundly new form of information processing isone of main subjects of quantum information physics.By now, many experimental realizations have been performed with optical systems [1-2], NMR techniques [3], superconducting device physics [4], electron physics [5], quantum dot [6-10], ion-trap [11] and cavity-QED technique [12] and so on, but today's implementation of quantum computer still meets serious challenges, such as quantum decoherence and quantum measurement, therefore many efforts have been made to design academic protocols based on different working laboratory devices.Since the seminal work of Loss and Divincenzo [7] and papers of Obermayer, Teich and Mahler [13], there has been increasing interest in quantum information processing (QIP) with quantum dots (QDs), which are propitious for integration and miniaturization. Subsequently, several theoretical proposals [14-16] for quantum teleportation (QT) of electron spin in a QD have been proposed due to the relative robustness of the electron spin against decoherence. Furthermore, with QDs placed in a microcavity and illuminated by laser beams, and with interaction between QDs mediated by a single-mode cavity field, the scheme of Imamoglu et al. [9] realizes controlled interactions between two distant QDs to a certain extent. We call such composite system as QDs-cavity system. It is worth noting that a crucial condition for a realization of QIP in such models is a strong coupling of a single QD to a single mode of microcavity (or nanocavity) of a high quality factor (high-Q). Quite recently, such random couplings [19-20] or even deterministic couplings [21] have been observed experimentally and the expansibility of quantum network, we focus onthe controlled quantum teleportation (CQT) of tripartiteGHZ-like state. CQT scheme was firstly proposed in1998 [22]. The feature of this scheme is that the teleportation between the sender and the receiver is under the control of the third party (the controller). In thisarticle, the  teleportation  scheme is based  on  QDscoupled through a microcavity mode and on the controlling nanostructure system composed of microcavity with QDs inside. The entanglement in microcavity is generated by the interaction between the electron spin and photon. Using single photon measurement [17, 23- 24], Faraday rotation [17, 23] and electron spin orientation measurement, the CQT can be implemented perfectly and we find that the success probability of the scheme can reach 1 if the cavities are switchable to choice the appropriate Faraday rotation angle. The article is organized as follows: we first briefly review the generation of the entangled state by Faraday rotation in QDs-cavity system, then propose the controlled teleportation scheme of tripartite GHZ-like state,which is under the control of a three-quantum-dot system.

 

2.Generation of the entangled state by Faraday rotation in QD-cavity system

When a photon interacts with an electron spin of QD in microcavity, the photon will excite two virtual processes in the microcavity and Faraday rotation will happen in these two virtual processes [17]. The virtual processes in Figure1 can be described as follow: For excess electron’s spin -↓, light of σ(z)- polarization excites an electron and a heavy hole (upper right), and light of σ(z)+  polarization excites an electron and a light hole (lower left). The final occupations of electron states in the dot are the same as the initial occupations, but a phase shift еis0hh of σ(z)-or еisolh of σ(z)+ will appear. Here  S0hh = ΩhhT   and  S0lh = ΩlhT  are for heavy and light hole respectively, Ωhh = Vhh2/ ħ2ωd = 3Vlh2/ ħ2ωd and  Ωlh = Vlh2/ ħ2ωd are the rates of Faraday rotation for these virtual transitions, is the detuning of the non-resonant photon, Vhh and Vlh are the transition matrix elements for exciting an electron and a heavy hole or an electron and a light hole in the Faraday rotation process and , T is the residence time of photon in microcavity. Therefore, under the basis , the full Hamiltonian of these processes in the rotation frame can be written as

 

 

 

 

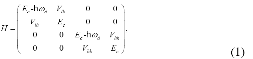
Where Ec is the energy of the excess electron. Similarly, if excess electron’s spin is↑, the corresponding Hamiltonian of these processes under the basis

  can be written as

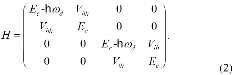
Since the dimension of QD is on the order of nanometer, if we place three QDs in a microcavity (Figure 2), it is possible that the total size of QD array is on the scale of nanometer and the wavelength of photon of several hundreds of nanometers is larger than the dimension of three-QD system. Therefore, when the pho-ton propagates into the microcavity, the single photon can interact with the cluster of three QDs simultaneously [23]. Meanwhile, the interaction produces a conditional single photon Faraday rotation [17, 23]. Now, we describe the Faraday rotation angle quantitatively and the generation of entanglement between electron spins and photon in QD-cavity system in detail. Suppose the original state of electron spins in QD system A is prepared as with quantization along z-direction and the photon propagates along the opposite of z-direction with linear polarization initially along the x-direction, i.e. the spin-photon wave-function before interaction can be written as

 

 

 

 

In order to distinguish clearly each step of the teleportation, we introduce the times 0 andT . The evolution state of the above system is in the Hilbert space with basis

 

 

 

 

 

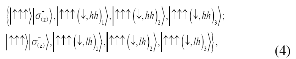
here, (↓hh) and (↓lh)express the electron-hole pair state excited inside of QD . The Hilbert space above is the direct sum of two subspaces: and . Either subspace under the evolution is closed. Considering the characteristic of orthogonality and linearity, we analyze two subspaces separately. In subspace , the corresponding Hamiltonian is

    

 

 

 

 

 

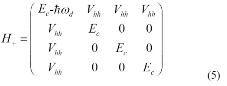
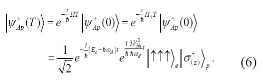
After the interaction between the initially unentangled photon with the spins in the three-QD system, the evolution state of the time T becomes

 

 

 

 

 

and the evolution state of the time T is

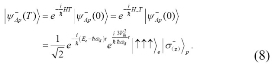
So the evolution state of the time T in the full space can be written as

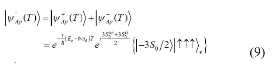
where , and , have been defined previously. Similarly, if the photon which is initially linearly polarized in the x-direction interacts with three QDs, which are prepared in , we can get the evolution state of the time T as

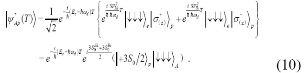
When the state of original spins in QDs of system A is prepared in the state , we can easily get the evolution state of the time T,

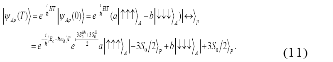
This means that spin-photon interaction in the microcavityA produces a conditional single-photon Faraday rotation around the z-axis by the angle and the angle can be changed by using a switchable cavity [12]. If the state of electron spin is , the linear polarization of the incoming photon is rotated the angle . Therefore, from formula (11), we find that Faraday rotation and entanglement between the electron spins and the photon are generated in QDs-cavity system, it can be used in the CQT in section III.

 

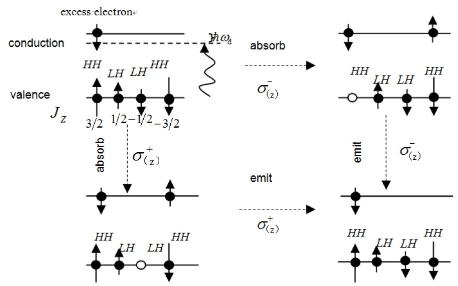
Figure 1.The virtual process will happen after the spin entangles with the photon in microcavity. For spin-↓ , light of σ(z)- polarization excites an electron and a heavy hole (upper right), and light of σ(z)+ polarization excites an electron and a light hole (lower left). denotes angular momentum quantum number.

 

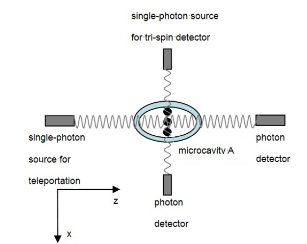
Figure 2.The generation of entanglement between electron spins and photon by Faraday rotation in QD-cavity system. Spin detection is performed by photon propagating along x.

 

3. The Controlled Quantum Teleportation Scheme of Tripartite GHZ-Like State in QDs-Cavity System

In this section, we describe in detail the CQT procedure of tripartite GHZ-like state encoded in the electron spins in the QD system. In order to realize the teleportation, the photon entangled with the three QDs in microcavity A propagates to microcavity C and then inte-racts with the QD in microcavity C. Subsequently, the photon which carries quantum information of QDs in microcavity A and of controlling system C travels from C to B and then interacts with the three QDs in micro-cavity B. The corresponding teleportation diagram is shown in Figure 3. In microcavity A, we consider , , a tripartite GHZ-like state [25-27], encoded in the electron spins which correspond to the three-QD system, while the control-ling system C is in , the QDs in destination system B is prepared in the other GHZ state [28-31] . In order to distinguish clearly each step of the teleportation, we introduce the times . Suppose the photon propagating in the z direction is initially linearly polarized in the x direction, so the original spin-photon wavefunction before interaction between the initial unentangled photon and the three entangled QDs in microcavity A is

After the interaction, the generalization of genuine four-particle entanglement between the single photon and the three entangled QDs encoded in the electron spin states is realized by the conditional Faraday rotation [17, 23] which depends on the photon polarization and spin orientation in QDs-cavity system A. According to section II, after neglecting overall phase factor, the evolution state of the composite system, composed of a single photon and three QDs in microcavity A, is

Subsequently, the photon with quantum information of three QDs in microcavity A travels to the controlling system C and then interacts with three QDs in system C, it will generate the entanglement between the above entangled four-particle state and the three entangled QDs in microcavity C. Before interaction, the composite system, composed of the single photon, the three entangled QDs in microcavity A and the three entangled QDs in the controlling system C, is in a state

After interaction, the state of the composite system becomes

 

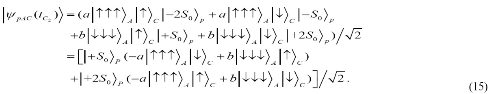
Finally, the photon with quantum information of four QDs in microcavity A and controlling system C propa-gates to the destination system B. Before interaction, the corresponding state of the composite system of photon, A, B and C is

After interaction, the state of the composite system becomes

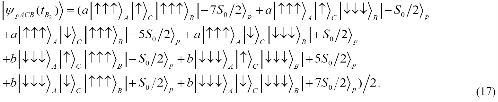
Then, we utilize the switchable cavity to achieve an appropriate Faraday rotation angle and the photon state can also be written as

Where

so the corresponding expression of the evolution state (17) could be written as

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

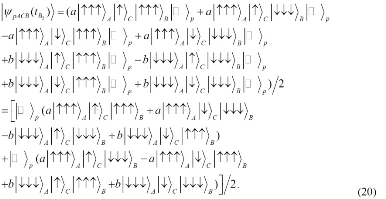
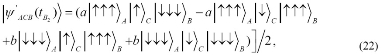
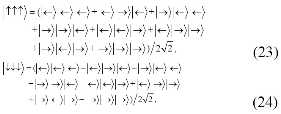
If the linear polarization of the photon is measured first, we will obtain the following two results with equal probability. Now, if we perform a measurement on the state of four QDs coming from microcavity A and the controlling system C, we cannot realize the CQT of tripartite GHZ-like state encoded in the electron spins of three QDs system in microcavity A to the three QDs in microcavity B through the controlling system C. Here, we implement a representation mapping for three-QD system A to complete the teleportation. In the representation, there are following mappings and the total state corresponding to (20) via the above mappings becomes

According to the above result, we can find if the li-near polarization of the photon is measured first, then the final measurement result will depend on spin orientation of four QDs in microcavity A and the controlling system C, after implementing spin measurement on three-QD system A and single-QD system C, the whole state will collapse to one of thirty-two states with equal probability. After communicating classically the outcome of the measurement, the destination receiver operates the corresponding quantum logic gate operation, the CQT can be realized successfully and the success probability of the scheme can reach 1 if the cavities are switchable to choice the appropriate Faraday rotation angle. For example, if the linear polarization state of the photon is , then the sender uses the spin detector to measure both the spin state in microcavity A and in the controlling system C. If the spin state in three-QD system A is and the spin state in the con-trolling system C is , the whole state will collapse to at once. Subsequently, the sender in-forms the classical information to the receiver, the receiver performs the local gate operation and he will get the state that the sender wants to transport. Here the fundamental gate operations in the microcavity are . Obviously, compared against more usual bipartite scheme, the tripartite CQT scheme can transport more information and expand quantum network. Similarly, the scheme in this article can be easily generalized to the CQT of multipartite GHZ-like state.

 

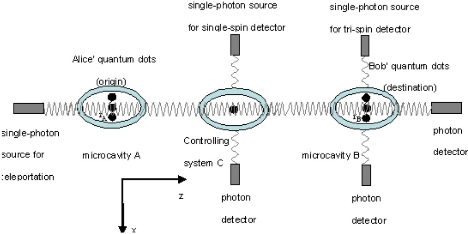
Figure3. Controlled teleportation of a triqubit GHZ-Like state teleports from microcavity A to microcavity B with the help of single quantum dot at controlling system C, the photon that travels in the z direction mediates this process. Tri-spin detection and single-spin detection are performed by photon propagating along x after they entangled in microcavities.

 

4. Conclusions

We have proposed the scheme for CQT of tripartite GHZ-like state encoded in the electron spins in QDs. A controlling system is introduced in the scheme, which participates the process of quantum teleportation as a supervisor. Without the cooperation of the controlling system, the teleportation can’t be realized. With the entanglement generating through the interaction be-tween the quantum dots in microcavities and a single photon, the CQT scheme can be realized by virtue of Faraday rotation, single photon detection and electron spin orientation measurement. The success probability of the teleportation scheme can reach 1 if the cavities are switchable to choice the appropriate Faraday rotation angle. Furthermore, we can realize the CQT of multipartite GHZ-like state with similar scheme in principle. The scheme is valuable not only for quantum security communication, large capacity quantum communication and large capacity information storage, but also for quantum distributed computation and quantum network. So far we have great challenges on quantum manipulation of photons and atoms, quantum decoherence and quantum measurement, so these subjects are worth studying further in future.

 

References

1. Nielsen MA, Knill E and Laflamme R. Complete quantum teleportation using nuclear magnetic resonance. Nature1998; 396: 52-55.doi:10.1038/23891
2. Awschalom DD, Loss D, and Samarth N. Semiconductor Spintronics and Quantum Computing (2002, Springer, New York).
3. Reina JH and Johnson NF. Quantum teleportation in a solid-state system. Phys. Rev.A2000;63:012303.doi:10.1103/Ph ysRevA.63.012303
4. Mooij JE, Orlando TP, Levitov L, Tian L, van der Wal CH, Lloyd S. Josephson Persistent-Current Qubit. Science 1999; 285: 1036. doi:10.1126/science.285.5430.1036
5. Platzman PM, Dykman MI. Quantum Computing with Electrons Floating on Liquid Helium. Science 1999; 284: 1967 – 1969. doi:10.1126/science.284.5422.1967
6. Tanamoto T. Quantum gates by coupled asymmetric quantum dots and controlled-NOT-gate operation. Phys. Rev. A 2000; 61: 022305. doi:10.1103/PhysRevA.61.022305
7. Loss D and DiVincenzo DP. Quantum computation with quantum dots. Phys. Rev. A 1998; 57: 120–126. doi:10.1 103/PhysRevA.57.120
8. Miranowicz A, Özdemir ŞK, Liu YX , Koashi M, Imoto N and Hirayama Y. Generation of maximum spin entanglement induced by a cavity field in quantum-dot systems. Phys. Rev. A 2002; 65: 062321. doi:10.1103/PhysRevA
9. Imamoglu A, Awschalom DD, Burkard G, DiVincenzo DP , Loss D, Sherwin M , and Small A. Quantum Information Processing Using Quantum Dot Spins and Cavity QED. Phys. Rev. Lett. 1999; 83: 4204–4207.doi:10.11 03/PhysRevLett.83.4204
10. Burkard G, Loss D and DiVincenzo DP. Coupled quantum dots as quantum gates. Phys. Rev. B 1999; 59: 2070–2078. doi:10.1103/PhysRevB.59.2070
11. Sørensen A and Mølmer K. Quantum Computation withIons in Thermal Motion. Phys. Rev. Lett. 1999; 82: 1971–1974. doi:10.1103/PhysRevLett.82.1971
12. Song KH and Zhang WJ. Proposal for teleporting an entangled coherent state via the dispersive atom–cavity-field interaction.Physics Letters  A 2001;  290: 214-218. doi:10.1016/S0375-9601(01)00691-0
13. ObermayerK ,Teich WG , and Mahler G. Structural basis of multistationary quantum systems. I. Effective single-particle dynamics.   Phys.Rev.B   1988;   37:   8096–8110. doi:10.1103/PhysRevB.37.8096
14. Visser RL and BlaauboerM .Deterministic Teleportation of Electrons in a Quantum Dot Nanostructure. Phys. Rev. Lett. 2006; 96: 246801. doi:10.1103/PhysRevLe tt.96.246801
15. Wang HF and Kais S. Quantum teleportation in one- dimensional quantum dots system. Chemical Physics Letters 2006; 421: 338-342. doi:10.1016/j.cplett.2006.01.093
16. Sauret O, Feinberg D and Martin T. Electron spin teleportation current through a quantum dot array operating in the stationary     regime.  Phys. Rev. B 2004; 69:035332. doi:10.1103/PhysRevB.69.035332
17. Leuenberger MN, Flatté ME and Awschalom DD. Teleportation of Electronic Many-Qubit States Encoded in the Electron Spin of Quantum Dots via Single Photons. Phys. Rev. Lett. 2005; 94: 107401.  doi:10.1103/PhysRevLett.94.10 7401
18. (a)Elzerman JM, Hanson R, Willems van Beveren LH, Witkamp B, Vandersypen L MK and Kouwenhoven LP. Single-shot read-out of an individual electron spin in a quantum dot. Nature 2004; 430: 431-435. doi:10.1038/nature02693 (b) Kroutvar M, Ducommun Y, Heiss D, Bichler M, Schuh D, Abstreiter G and Finley JJ. Optically programmableelectron spin memory using semiconductor quantum dots. Nature 2004; 432: 81-84. doi:10.1038/nature03008
19. Reithmaier JP, S k G, Löffler A, Hofmann C, Kuhn S, Reitzenstein S, Keldysh LV, Kulakovskii VD, ReineckeTL and Forchel A. Strong coupling in a single quantum dot–semiconductor microcavity system. Nature 2004; 432:197-200. doi:10.1038/nature02969
20. Yoshie T, Scherer A, Hendrickson J, Khitrova G, GibbsHM, Rupper G, Ell C, Shchekin OB and Deppe DG. Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 2004; 432: 200-203.  doi:10.1038/nat ure03119
21. Badolato A, Hennessy K, Atatüre M, Dreiser J, Hu Evelyn, Petroff PM, Imamolu A. Deterministic Coupling of Single Quantum Dots to Single Nanocavity Modes. Science 2005;308: 1158 – 1161. doi:10.1126/science.1109815
22. Karlsson  A  and  Bourennane  M.  Quantum  teleportation using three-particle entanglement. Phys. Rev. A 1998; 58:4394–4400. doi:10.1103/PhysRevA.58.4394
23. Leuenberger MN. Fault-tolerant quantum computing with coded spins using the conditional Faraday rotation in quantum dots. Phys. Rev. B 2006; 73: 075312.  doi:10.1103/PhysRevB.73.075312
24. (a) Ionicioiu R and Popescu AE. Single-spin measurement using spin–orbital entanglement. New J. Phys. 2005; 7:120.   doi:10.1088/1367-2630/7/1/120; (b) Rugar D, Budakian R, Mamin HJ and Chui BW. Single spin detection by magnetic resonance force microscopy. Nature 2004; 430:329-332. doi:10.1038/nature02658; (c) Santori C, FattalD, Vukovi J, Solomon GS and Yamamoto Y. Indistinguishable photons from a single-photon device. Nature 2002;419: 594-597. doi:10.1038/nature01086
25. (a) Sagi Y. 2003 New scheme for generating GHZ like state of $n$ photons. (Preprint quant-ph/0307097) Phys. Rev. A 2003; 68: 042320. (b) Liang LM, Chen PX, Li CZand  Huang MQ. Purification of multipartite entangled mixed states under local manipulation. Phys. lett. A 2002;294: 71-73.
26. Zhang J and Braunstein SL. Continuous-variable Gaussian analog of cluster states. Phys. Rev. A 2006; 73: 032318. doi:10.1103/PhysRevA.73.032318
27. Cabello A. Multiparty multilevel Greenberger-Horne-Zeilinger states. Phys. Rev. A 2001; 63: 022104. doi:10.1103/PhysRevA.63.022104
28. Guo GP, Zhang H ,Guo GC. Quantum Non-DemolitionBell State Measurement and N-party GHZ State Preparation in Quantum Dot. (Preprint quantph/0511242) Modern Physics Letters B 2007; 21: 867-874.
29. Lu CY, Zhou XQ, Guhne O, Gao WB, Zhang J, Yuan ZS,Goebel A, Yang T and Pan JW. Experimental entanglement of six photons in graph states. Nature Physics 2007;3: 91-95.
30. Zhao Z, Chen YA, Zhang AN, Yang T, Briegel HJ. AndPan JW. Experimental demonstration of five-photon entanglement and open-destination teleportation. Nature, 2004; 430: 54-58. doi:10.10 38/nature02643
31. Pan JW, Daniell M, Gasparoni S, Weihs G and Zeilinger A. Experimental Demonstration of Four-Photon Entanglement and High-Fidelity Teleportation. Phys. Rev. Lett. 2001; 86: 4435–4438. doi:10.1103/PhysRevLett.86.4435

 

Received 20April,2010;accepted 8June, 2010;published online26June,2010.

 

Copyright:(C)2010K. Hu et al.This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.