Article
Application of Rotatable Central Composite Design in the Preparation and Optimization of Poly (Lactic-co-Glycolic Acid) Nanoparticles for Controlled Delivery of HAS
Hua Song 1, Xiufeng Cao2, Jing Ruan1, Xia Peng3, Juan Wang3, Can Wang4, Chenchen Bao1
1Department of Bio-Nano Science and Engineering, National Key Laboratory of Nano/Micro Fabrication Technology, Key Laboratory for Thin Film and Microfabrication of Ministry of Education, Institute of Micro-Nano Science and Technology, Shanghai Jiao Tong University, Shanghai 200240, People’s Republic of China
2Department of Physics and Institute of Theoretical Physics and Astrophysics, Xiamen University, Xiamen 361005, China
3Department of Laboratory Medicine, Shanghai First People’s Hospital, Shanghai Jiao Tong University, Shanghai 200080, People’s Republic of China
4Xiangya School of Medicine, Central South University, Changsha 410012, People’s Republic of China
* Corresponding author: songhua@sjtu.edu.cn Tel: +86 210 34206375; Fax: +86 021 34206886
The purpose of this work was to obtain an optimized Human Serum Albumin (HSA)-loaded poly(lactic-co-glycolic acid)(PLGA) nanoparticles (NPs). A rotatable central composite design (RCCD) was applied to evaluate the joint influence of three formulation variables: the duration time of homogenization, agitation speed of homogenization, and volume ratio of organic solvent phase to external aqueous phase. The experimental datum allowed the development quadratic models (P<0.05) describing the inter-relationship between the dependent and independent variables. To enhance the protein content and minimize the particle size of the NPs simultaneously, a response surface methodology was employed. By solving the regression equation, and analyzing the response surface contour and plots, the optimal conditions for the preparation of HSA-loaded NPs were found to be: the duration time of homogenization was 4 min, the agitation speed of homogenization was 3.5 krpm and the volume ratio of organic solvent phase to external aqueous phase was 0.6. The entrapment efficiency (E.E.) was 54.52±5.86% and the average particle size is 252.7±17.90 nm. The NPs, as examined by scanning electron microscopy (SEM), have a smooth and spherical surface and particle sizes are less than 500 nm. The results indicated that RCCD represents an ideal and potential technique for NPs preparation optimization.
Keywords: RCCD, PLGA, HSA, Nanoparticles
Citation: H. Song et al, Application of Rotatable Central Composite Design in the Preparation and Optimization of Poly(Lactic-co-Glycolic Acid) Nanoparticles for Controlled Delivery of HSA, Nano Biomed. Eng. 2011, 3(1), 34-41.
DOI: 10.5101/nbe.v3i1.p34-41.
Due to rapid progress in biotechnology and gene technology, a large number of potential therapeutic proteins, as well as peptides, are gaining increased interest as drug molecules [1-3]. Therefore, formulation and development of suitable drug delivery systems makes protein delivery an important area of research. Biodegradable polymeric nanoparticles (NPs) as injectable depots for protein and peptide drugs have been extensively investigated for the past two decades. As an ideal biocompatible and biodegradable copolymer, Poly (D, L-lactic-co-glycolic acid) (PLGA) [4], has been mostly used for delivering protein drugs. Various proteins have been encapsulated within PLGA NPs using different formulation methods. In the previous studies, the most commonly used method is the solvent evaporation technique, which based on the formation of a double emulsion (water-in-oil-in-water) (W/O/W) [5]. W/O/W is a complex procedure as it involves several processing variables and design components, in the formulation, even slight changes of these variables and system components can have significant impact on the quality of final product [6]. In order to get the NPs with ideal particle size and entrapment efficiency, it is necessary to optimize the operating conditions. It is of highest importance in case of drugs like protein, where the cost is usually very high. Complex designs such as rotatable central composite design (RCCD) can be applied for the optimization [7]. In the present study, human serum albumin (HSA)-containing PLGA NPs providing controlled drug delivery were prepared using a double emulsion technique. RCCD and Response surface methodology (RSM) were used to investigate and optimize the impact of critical factors namely volume ratio of organic solvent phase to external aqueous phase, agitation speed, duration of homogenization on the response properties such as mean particle size and entrapment efficiency. In addition, the optimized HSA-containing PLGA NPs were characterized by dynamic laser light scattering (DLLS), scanning electric microscope (SEM) and assessed for in vitro drug release. The optimized NPs would be given as an ideal protein prolonged release delivery system and would be beneficial in better control of therapy with protein drugs.
Tween® 80 (polyoxyethylene sorbitan monooleate), Poly(vinyl alcohol) (PVA) (Mw 14–16 kDa) and HSA was purchased from Sigma-Aldrich (Shanghai, China). PLGA with a monomer ratio (lactic acid/glycolic acid) of 50:50 was purchased from Daigang Biomaterial Co., Ltd (Jinan, China). BCA protein assay kit was purchased from Pierce Chemicals (Rockford, IL, USA). All other reagents were purchased from Sigma-Aldrich.
PLGA NPs containing HSA (50 μg permg of NPs) were prepared by the double emulsion-solvent evaporation technique based on the method of Liao et al. Briefly, 20 mg of PLGA were dissolved in appropriate amount of dichloromethane. This polymer solution was injected into 100 μl of phosphate-buffered saline, pH7.4 (PBS7.4) as the inner aqueous phase (W1) containing HSA. Next, the previously formed inner emulsion (W1/O) was generated by a high-speed homogenizer of IKA ultra turrax operating at 3,000 rpm for 2 min. After this step, the first emulsion was injected into 10 ml outer aqueous phase (W2), which composed of aqueous 1.5% (w/v) PVA and 2% Tween80, resulting in a multiple emulsion (W1/O/W2), which was homogenized by ultra turrax at specific speed and time following an incubation on ice. This emulsion was put on a rota-evaporator under vacuum (500mHg) for 3 h at room temperature for complete solvent evaporation. The organic phase was evaporated leading to precipitation of polymer to get the NPs, which hardens with time. The NPs were collected by centrifugation at 10,000×g for 5min at 4 °C and washed with distilled water three times followed by freeze-drying using mannitol as cryoprotectant (PLGA:Mannitol:100:30) to get dry powder containing NPs.

Table 1. Independent variables and their coded levels investigated in RCCD
Note: X1 represents duration of homogenization (min); X2 represents agitation speed (krpm); X3 represents volume ratio of organic solvent phase to external aqueous phase (V/V);
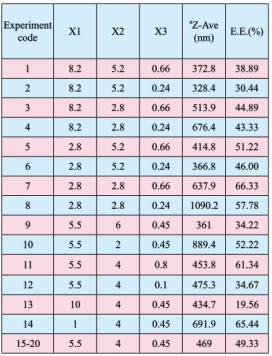
Table 2. RCCD matrix with coded level and measured responses of the evaluated factors of protein-loaded NPs (n=3).
Note: X1 represents duration of homogenization (min); X2 represents agitation speed (krpm); X3 represents volume ratio of organic solvent phase to external aqueous phase (V/V); aZ-Ave represents average particle size diameter; E.E. represents encapsulation efficiency.
RCCD was implemented for the optimization of various response properties. Initially, preliminary studies were conducted to determine the critical factors involved in NPs preparation using double emulsion technique. Based on preliminary studies, three critical factors namely volume ratio of organic solvent phase to external aqueous phase, agitation speed, duration of homogenization were selected for the optimization of mean particle size and entrapment efficiency. Upper and lower limits for the individual factors, with which stable NPs can be prepared, were identified in the preliminary studies. During the optimization trials, these values for critical factors were varied between the extreme levels as indicated in Table 1. In general, RCCD needs a total of (2k+2k+n) individual experiments, where k is the number of factors and n is the number of experiments carried out at center points to evaluate experimental reproducibility. The first set involved 2k experiments forming the main factorial design and second set involved 2k experiments, which were carried out at the star points, a distance(±α(2k/4)) away from the center. For three controlled variables in this study, the design is performed with 2 points from the original factorial design, 2×3 axial points at a distance with α= ± 1.68 from the center point, and six center points for estimating the experimental error. Thus, a set of 20 experimental points were needed to determine the model coefficients and the schematic representation of this design can be found in Table 2.
2.4 Characterization of nanoparticles
The mean diameter and particle size distributions of the optimized NPs were determined by dynamic light scattering measurement using a NICOMP 380 ZLS Zeta Potential/Particle Sizer (PSS Nicomp, Santa Barbara, CA, USA) equipped with a 5 mW heliumneon laser at a wavelength of 633 nm and 90° scattering angle. For each measurement, 2 mg of formulation was dispersed in 10 mL of previously sonicated and filtered ultra-pure water. Obtained homogenous dispersion was immediately used for the determination of mean particle diameter. The data acquisition and processing was performed using ZPW388 software (NICOMP Instruments Inc.). The morphological examination of NPs was performed using a scanningelectron microscope (SEM, Carl Zeiss SMT, Oberkochen, Germany). In practice NPs were mounted onto metal stubs using double-sided adhesive tape. After being vacuum-coated with a thin layer (100–150Å) of gold, the NPs were examined by SEM at 15 or 20 kV.
The NPs encapsulation efficiency was determined upon their separation from the aqueous preparation medium containing the non-associated protein by centrifugation (20,000×g, 4 °C, 10 min). The amount of free protein was determined in the supernatant by using a bicinchoninic acid (BCA) assay. The extraction procedure was performed a total of 3× for each particle type. The NPs encapsulation efficiency (E.E.) was calculated using the following equation: E.E. (%)=[(Total protein amount-Free protein amount)/ Total protein amount]×100% (1)
In vitro release study of optimized NPs formulation was evaluated in buffer solution. Briefly, 100 mg of freeze dried NPs were suspended in 20 mL phosphate buffer saline (PBS) at pH 7.4 and at 37°C, which previously filtered on 0.22 μm sterile filters and microbiologically preserved with 0.02%w/w sodium azide. Then the release medium were placed in a thermostatic bath at 37°C. At scheduled time intervals, the release medium was withdrawn and replaced with the equal volume of fresh filtered medium. Samples were centrifuged (20,000×g, 4°C, 10 min) and the supernatant was analyzed for HSA content using BCA protein assay kit following the manufacturer's protocol. Results are expressed as cumulative release of HSA from NPs of three replicates. The obtained in vitro release data were fitted into conventional (zero order [8], first order [9], Higuchi [10], Ritger-Peppas model [11]) and novel (reciprocal-powered time [12]) mathematical models for evaluation of release kinetics. The parameters of release kinetics regression coefficient (R) were calculated for the best-fit model. Following mathematical models were used for the drug release data fitting:
where, F is the fraction of drug released up to time t, k0, kf , kH, kR, a, m, and b are the model parameters.
For analyzing the influence of multiple factors, a mathematical polynomial equation model of design was established. A quadratic model expressed as following equation was used to correlate the theoretical response (Y) to the coded variables (X). where β0, βi, βii, andβij are the regression coefficients, for intercept, linear, quadratic, and interaction terms, respectively.
![]()
The polynomial equation obtained for each response property was analyzed using RSM. The optimum levels of the selected variables were obtained by solving the regression equation and also by analyzing the response surface contour and surface plots. In addition, statistical tests, such as analysis of variance (ANOVA), were performed to determine the statistical significance of each model with STATISTICA 6.0 software.
The factorial design is frequently used for the planning of a research because it provides the maximum amount of information and requires the least amount of experiments. The use of factorial design is the most rational and scientific way for simultaneous identification, estimation, and analysis of influence of critical factors on the quality of final system. RCCD consists of embedded factorial design, group of star points for the estimation of curvature, and center points for the determination of experimental reproducibility. RCCD allows the estimation of all the regression parameters required to fit a second order model to a given response. Moreover, use of RCCD aids in identification of explanatory variables and their first-order interactions, and a mathematic model can be established based on the input variables and the given responses. RCCD constitutes optimization method, which can offer possibility of analyzing larger number of variables at more levels with very few experimental runs. Although the traditional optimization method of experimental design to optimize operating conditions is by changing one variable at a time, which is time- consuming and may ignore the interactions between variables. RSM can overcome these limitations, since it is a rapid technique used to empirically derive a functional relationship between an experimental response and a set of input variables[13]. When cost and time of each experiment is very high, use of RSM optimization method can help in analyzing first-order and second-order interactions. Thus, it may determine the optimum level of experimental factors required for a given response and define the interactions between factors and prevent doing unnecessarily numerous runs. In the present design, RCCD and RSM were successfully implemented for the optimization of various quality attributes of PLGA NPs. Preparation of NPs is a complex procedure, unique attributes of NPs like particle size and entrapment efficiency are of most importance from the biological and pharmaceutical point of view[14, 15]. Particles with smaller average diameter showed slower release, because smaller particles are generally formed with higher impact [16]. The compact structure of smaller particles varies the tortuous polymeric diffusion pathways[17]. This ultimately leads to a sustained diffusion of drug from the particles. Another quality attribute of NPs is the entrapment efficiency as it should be properly optimized to avoid the loss of drug during processing. Here we choose the particle diameter and the entrapment efficiency as the experiment investigation response.
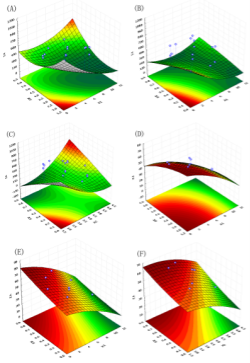
Fig. 1. Response surface plots of mean particle size (Y1) and entrapment efficiency (Y2) versus three factors (third factor was held at optimum level: X1 = duration of homogenization (min), X2 = agitation speed (krpm), X3 = volume ratio of organic solvent phase to external aqueous phase (V/V).
Mean particle size
The size of the particles is a very important parameter, because it is one of the factors that control the kinetics of drug [18, 19]. The mean particle size of various formulations is shown in Table 2. It can be seen from the results that the particle size ranged between 328.4 and 1090.2 nm, which indicating the sensitivity toward the critical factors studied. The particle size has a range of three fold suggesting the fine control of the selected factors to get optimum particle size. The obtained data were fitted in quadratic model to describe the relationship between critical factors and response. The results are shown in Equation (8):

The regression coefficient (R) of this equation was found to be 0.9817, which indicating the good correlation between response and selected factors. P<0.01 indicates the quadratic model is highly statistically significant. The obtained polynomial equation was used for RSM and three-dimensional surface plots were generated (Fig.1). It can be seen from Fig. 1 that duration of homogenization, agitation speed and volume ratio of organic solvent phase to external aqueous phase have considerable effect on the mean particle size. Fig. 1A shows that an increase in the duration and intensity of homogenization within limits lead to the remarkable decrease in the mean particle size. But the excessive homogenizations lead to the agglomeration of the small particles, and increase the mean particle size remarkably. This may be due to the fact that excess dispersion leads to increase in viscosity of polymer solution. High viscosity of polymeric solution slows down the rapid dispersion of organic phase into aqueous phase resulting in the formation of bigger aggregates. It is clear from Fig. 1B that increase the duration of the homogenization and increase volume ratio of organic solvent phase to external aqueous phase can all decrease the mean particles size. Fig. 1C indicates an interaction relationship between homogenization speed and volume ratio of organic solvent phase to external aqueous phase. While a typical saddle fitting of Fig. 1C indicate that optimum particle size can be achieved by taking suitable homogenization speed and volume ratio of organic solvent phase to external aqueous phase. Higher homogenization speed coupled with very high volume ratio of organic solvent phase to external aqueous phase lead to dramatic increase in the mean particle size.
Entrapment efficiency
The entrapment efficiencies of individual batches of prepared formulations are presented in Table 2. The entrapment efficiency ranged between 19.56% and 66.33%, which indicate that the response was sensitive toward the studied factors. The selected quadratic model was used to generate the following second-order polynomial equation for the entrapment efficiency:

The results of ANOVA indicate that the selected quadratic model well-describes the relationship between the entrapment efficiency and critical factors with P<0.05. The regression value of the above equation was found to be 0.9516 indicating suitability of the selected model. Equation (9) was also used to generate three- dimensional response surface plots by keeping one factor at optimum level. Out of the three factors studied, duration of homogenization, and volume ratio of organic solvent phase to external aqueous phase were found to have considerable effect on the mean particle size. Fig. 1D indicates the relationship between duration of homogenization, agitation speed and entrapment efficiency. An increase in duration of homogenization or agitation speed all resulted in proportionate decrease in the entrapment efficacy. Even though P-value in Equation (9) did not show dramatically statistical significance, it can be seen from Fig. 1E and Fig. 1F that increase in volume ratio of organic solvent phase to external aqueous phase increased the entrapment efficiency. This increase can be due to the fact that organic solvent phase acts as disperse medium for drug to entrap drug into the polymeric matrix forming NPs. However, if the amount of organic solvent is increased beyond an optimum value, no NPs will be achieved due to excess organic solvent easily achieved phase inversion. The optimum points for NPs preparation were obtained by graphic method and partial derivative resolution of Equations (8) and (9), at which mean particle size and highest drug entrapment efficiency were expected to be achieved with comprehensive consideration. In addition, the optimum zone for NPs preparation can be found readily from Fig. 2 (obtained by overlapping Fig. 1A and 1D), Fig. 3 (obtained by overlapping Fig. 1B and 1E) and Fig. 4 (obtained by overlapping Fig. 1C and 1F). It was suggested that duration of homogenization (4), agitation speed (3.5) and volume ratio of organic solvent phase to external aqueous phase (0.6) should be employed for the practical preparation. At the recommended conditions, 196.62 nm of mean particle size and 60.03% of entrapment efficiency were expected to be achieved according to Equations (8) and (9). The adequacy of the predicted models was examined by additional independent experiments at the suggested optimal preparation conditions. Each formulation was prepared three times, and the mean particle size and entrapment efficiency were estimated. Under the suggested optimum conditions, the actual average value of 252.7±17.9 nm of mean particle size and 54.52±5.86% of entrapment efficiency were obtained (n=3). Even though the error value obtained for entrapment efficiency is lesser, distinct deviations were observed for mean particle size. This may be due to the presence of some minor contributing factors, which were not considered during the experiment. It could be seen that the size distribution was relatively narrow (Fig. 5). The SEM study (Fig. 6) shows smooth, homogeneous and spherical shaped spheres in nano range and there is no aggregation after lyophillization in case of the optimum conditions. About more than 90% particles were found to have diameter below 500 nm. The average particle size was about 300nm, and the densest and narrowest range of particle dispersion was noticed between 100 nm and 400 nm. Thus, the optimized NPs preparation for mean particle size and drug loading efficiency were successfully developed by RCCD and RSM. The in vitro drug release profile of optimized NPs formulation is presented in Fig. 7. The NPs formulation provided a sustained drug release pattern, which was characterized by an initial burst release of HSA followed by a slow and continuous drug release for 60 days. The initial burst release may be attributed to the dissolution of entrapped HSA from the surface of small NPs. The later phase providing a slow release may have been resulted from slow dissolution and diffusion of the entrapped HSA from the polymeric matrix of NPs. The drug release kinetics was studied by fitting the data into various mathematical models. The regression analysis indicated that drug release from NPs can be well explained by reciprocal-powered time model (R = 0.9958) compared with zero-order kinetics (R= 0.9061), first-order kinetics (R= 0.9390), Higuchi kinetics (R= 0.9727) and Ritger Peppas (R=0.9905, n=0.30). In the previous study, Barzegar-Jalali have reported that the reciprocal-powered time model is the most suitable model to study the drug release kinetics from NPs formulations [20]. It has also been found in Ritger Peppas model that the exponent (n) could be less than 1/2 (Fick diffusion)[21]. This reveals that there are some common-grounds existing between various controlled release mechanisms. A typical feature from various controlled releases is that the extraction of drug from the polymeric matrix is a result of solvent penetration.
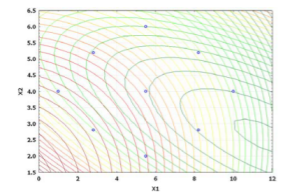
Fig. 2. Overlapped contour plot for duration of homogenization (min) and agitation speed (krpm)

Fig. 3. Overlapped contour plot for duration of homogenization (min) and volume ratio of organic solvent phase to external aqueous phase (V/ V)
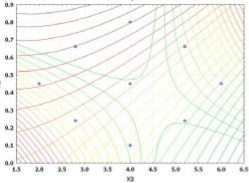
Fig. 4. Overlapped contour plot for agitation speed (krpm) and volume ratio of organic solvent phase to external aqueous phase (V/V)
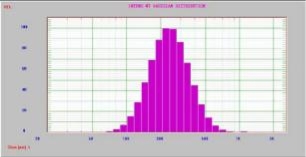
Fig. 5. Intensity mean diameter distributions of HSA-loaded PLGA NPs (Gaussian distribution).

Fig. 6. Scanning electron microscopic (SEM) images of HSA-loaded NPs
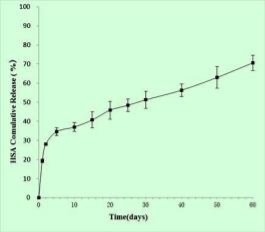
Fig. 7. In vitro cumulative release of HSA from PLGA NPs in PBS at pH 7.4 and 37°C(n=3).
4. Conclusions
In the present study, HSA-containing PLGA NPs providing controlled protein delivery system were prepared. RCCD and RSM were used to investigate and optimize the impact of critical factors on the response properties of mean particle size and entrapment efficiency. The optimized formulation provided a uniform small particle size with high entrapment efficiencies. Moreover, the optimized HSA-containing PLGA NPs were characterized by DLLS and SEM. In vitro drug release study confirmed that the entrapped protein is released over 60 days in a controlled manner. Based on these findings, the proposed NPs formulation may be given as an ideal protein prolonged release delivery system and would be beneficial in better control of therapy with protein drugs.
This work is supported by the National Key Basic Research Program (973 Project) (2010CB933901), National 863 Hi-tech Project (2007AA022004), Important National Science & Technology Specific Projects (2009ZX10004-311), National Natural Scientific Fund (No.10904126), Fujian Province Natural Science Foundation (No. 2009J05014), Special project for nanotechnology from Shanghai (No. 1052nm04100), New Century Excellent Talent of Ministry of Education of China (NCET-08-0350), Shanghai Science and Technology Fund (10XD1406100). The authors appreciated the support from the Instrumental Analysis Center of Shanghai Jiao Tong University in the part of the samples analysis.
1. Liu C. Research and development of nanopharmaceuticals in China. Nano Biomed. Eng. 2009,1(1):1-12. doi:10.5101/nbe.v1i1.p1-12
2. Agyei D, Danquah MK. Industrial-scale manufacturing of pharmaceutical-grade bioactive peptides. Biotechnol. Adv. 2011,29 (3):272-277. doi:10.1016/j.biotechadv.2011.01.001
3. Andrade F, Videira M, Ferreira D, et al. Nanocarriers for pulmonary administration of peptides and therapeutic proteins. Nanomedicine. 2011,6(1):123-141. doi:10.2217/nnm.10.143
4. Liao X, Wang J, Zhang H. Preparation Poly (lactide-co-glycolide) Microsphere of Bone Sialoprotein. Nano Biomed. Eng. 2010,2 (2):133-137. doi: 10.5101/nbe.v2i2.
5. Kirby G, White L, Rahman C, et al. PLGA-based microparticles for the sustained release of BMP-2. Polymers. 2011. doi:10.3390/ polym3010571
6. Tian F, Prina-Mello A, Estrada G, et al. Macrophage cellular adaptation, localization and imaging of different size polystyrene particles. Nano Biomed. Eng. 2009,1(1):13. doi: 10.5101/nbe.v1i1. p13-26
7. Bajic D, Jozic S, Podrug S. Design of Experiment¡¯s Application in the Optimization of Milling Process. Metalurgija. 2010,49(2):123- 126.
8. Rastogi A, Luo Z, Wu Z, et al. Development and characterization of a scalable microperforated device capable of long-term zero order drug release. Biomedical microdevices. 2010:1-7. doi:10.1007/s10544-010-9446-x
9. Brandl F, Kastner F, Gschwind RM, et al. Hydrogel-based drug delivery systems: Comparison of drug diffusivity and release kinetics. Journal of Controlled Release. 2010,142(2):221-228. doi:10.1016/j.jconrel.2009.10.030
10. Elzoghby AO, El-Fotoh WSA, Elgindy NA. Casein-based formulations as promising controlled release drug delivery systems. Journal of Controlled Release. 2011. doi:10.1016/j.jconrel.2 011.02.010
11. Li C, Cheng L, Zhang Y, et al. Effects of implant diameter, drug loading and end-capping on praziquantel release from PCL implants. International journal of pharmaceutics. 2010,386(1-2):23-29.
12. Mohammadi G, Barzegar-Jalali M, Valizadeh H, et al. Reciprocal Powered Time model for Release Kinetic Analysis of Ibuprofen Solid Dispersions in Oleaster Powder, Microcrystalline Cellulose and Crospovidone. Journal of pharmacy & pharmaceutical sciences: a publication of the Canadian Society for Pharmaceutical Sciences, Socit canadienne des sciences pharmaceutiques. 2010,13(2):152.
13. Song H, Chen J M, Liang H J, et al. Optimized preparation of Docetaxel Polysorbate 80/Phospholipid Mixed Micelles Injection by Uniform Design. Chinese Pharmaceutical journal. 2008,43 (17):1327-1332.
14. Chen F, Huang P, Mo X. Electrospinning of Heparin Encapsulated P (LLA-CL) Core/Shell Nanofibers. Nano Biomed. Eng. 2010, 2(1):84.
15. Anton E, Swetha K, Thomas W, et al. Dextran-based Nanocarriers as Efficient Media Delivery Vehicles to Cell Production Bioreactors. Nano Biomed. Eng. 2010,2(2):126.
16. Chen Y, Chen Y, Chen W, et al. Evolution of phase morphology of high impact polypropylene particles upon thermal treatment. European Polymer Journal. 2007, 43(7):2999-3008. doi:10.1016/ j.eurpolymj.2007.04.026
17. Zhang K, Wang Y, Hillmyer MA, et al. Processing and properties of porous poly(-lactide)/bioactive glass composites. Biomaterials. 2004,25(13):2489-2500. doi:10.1016/j.biomaterials.2003.09.033
18. Song H, He R, Wang K, et al. Anti-HIF-1 alpha antibody-conjugated pluronic triblock copolymers encapsulated with Paclitaxel for tumor targeting therapy. Biomaterials. 2010,31(8):2302-2312. doi:10.1016/ j.biomaterials.2009.11.067
19. Song H LB, Du T,Jiang L,Yang H, He R,Gao F, Cui DX. Preparation and characterization of PTX-HIF-1-immunomicelles with active carboxylic terminals. IEEE-NANOMED. 2008:ID:35.
20. Barzegar-Jalali M. Kinetic analysis of drug release from nanoparticles. Journal of Pharmacy & Pharmaceutical Sciences. 2008,11(1):167-177.
21. Krupa I, Nedelcev T, Chorvat D. Glucose diffusivity and porosity in silica hydrogel based on organofunctional silanes. European Polymer Journal. 2011:Article in Press. doi:10.1016/ j.eurpolymj.2011.02.011
Copyright:(c) 2011 H. Song, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.