Research Article

 

A Multi-Layer Finite Element Model Based on Anisotropic Hyperelastic Fiber Reinforcements within Intestinal Walls

 

Dasheng Liu 1, 2, 3*, Guozheng Yan 1, 3

 

1 Department of Instrument Science and Engineering, School of Electronic Information and Electrical Engineering, Shanghai JiaoTong University, Shanghai, 200240, China.

2 National Center for Translational Medicine, Collaborative Innovational Center for System Biology, Shanghai Jiao Tong University, Shanghai 200240, China.

3  Shanghai Engineering Research Center for Intelligent diagnosis and treatment instrument, Shanghai 200240, China.

 

* Corresponding authors. E-mail: dsliu@sjtu.edu.cn

 

Received: Oct. 18, 2017; Accepted: Nov. 28, 2017; Published: Dec. 8, 2017

 

Citation: Dasheng Liu, and Guozheng Yan, A Multi-Layer Finite Element Model Based on Anisotropic Hyperelastic Fiber Reinforcements within Intestinal Walls. Nano Biomed. Eng., 2017, 9(4): 291-297.

DOI: 10.5101/nbe.v9i4.p291-297.

 

Abstract

The intestinal wall is considered as a highly composite heterogeneous tissue characterized by a strong nonlinear stress-strain passive response with an exponential stiffening effect at higher deformations. The conventional theory of fiber-reinforced elastic solids allows one to describe the anisotropic strain energy as a function of the pseudo-invariants arising from the coupling of the elastic deformation and the direction of fiber reinforcement. In this paper, a multi-layer finite element model of the intestine walls is developed, based on an anisotropic hyperelastic theory of the layered structure, in which each layer may be considered as a composite reinforced by two families of fibers that are arranged in symmetrical spirals. A potential is proposed to model the intestine walls as a fiber-reinforced composite consisting of two directions of muscle-fiber reinforcement and a cross-ply collagen arrangement. Moreover, finite element simulations of a specimen cut from the intestinal walls were carried out by using the same form of strain-energy function, described by a well-known Gasser-Ogden-Holzapfel (GOH) model, for each layer. The model parameters were optimized by fitting the model to the experimental stress-stretch responses in both longitudinal and circumferential directions. In order to verify the proposed model, finite element analyses were carried out to investigate the distributions of equivalent stress in the intestine after the complete deployment of capsule robot legs.

 

Keywords: Hyperelastic; Intestinal walls; Finite element model; Multi-layer composite; Anisotropic; Fiber reinforcements

Introduction

In human anatomy, the intestine is the segment of the gastrointestinal (GI) tract extending from the pyloric sphincter of the stomach to the anus and, consists of two segments, the small intestine and the large intestine. The capsule endoscopy has been the most effective medical device to examine the GI tract painlessly and non-invasively, but the passive feature of capsule endoscopy makes it out of control in the intestine [1]. In recent years, many researchers have been engaging in developing a capsule robot using various driving mechanisms [2-5]. The capsule robot, which can examine the whole GI tract non-invasively and actively, is one of the most representative medical devices. However, the imperfection of model between the capsule robot and the intestine has been one of the biggest obstacles of the development of the capsule robot [6]. The intestinal is a highly composite heterogeneous tissue characterized by a strong nonlinear stress-strain passive response with an exponential stiffening effect at higher deformations. Since many concerns such as cost and safety, it is hard to perform experimental investigations inside the body whenever the data is required for the endoscope design. In the past few years, there has been a significant growth in research in the mechanical properties of biological soft tissue treated from the continuum mechanical perspective [7-15]. Among of them, Holzapfel et al. [7] proposed a new constitutive model, referred to as the Holzapfel-Gasser-Ogden (HGO) model, for the description of the mechanical response of arterial tissue. The artery is modeled as a thick-walled nonlinearly elastic circular cylindrical tube consisting of two layers corresponding to the media and adventitia. Then, Holzapfel [8] developed an approach that allows the determination of material models from uniaxial tests and histostructural data including fiber orientation of the tissue. A combination of neo-Hookean and Fung-type strain-energy functions is utilized, and inequality constraints imposed on the constitutive parameters are derived providing strict local convexity and preferred fiber orientations. In order to correctly model compressible anisotropic behaviour, Nolan et al. [10] presented a modified anisotropic (MA) model, whereby the full anisotropic invariants are used, so that a volumetric anisotropic contribution is represented, and developed a finite element user-defined material subroutine for the simulation of stent deployment in a slightly compressible artery. Through progress in medical imaging, image analysis and finite element methods, it is now possible to construct in vivo patient-specific geometries and thus to study specific, clinically relevant problems in arterial mechanics via FE simulations [16, 17]. Pierce et al. [16] presented a pragmatic methodology to simultaneously account for both the three-dimensional residual stress distributions in the arterial tissue layers, and the equilibrium of the in vivo patient-specific geometry with the known boundary conditions. The development of an anatomically realistic model of the intestinal walls is essential for the progress of the clinical applications of medical robotics. The macroscopic mechanical behavior of the intestinal tissue is characterized by anisotropy, viscoelasticity and a nonlinear stress-strain relationship. A structurally-motivated constitutive model for the intestine has been developed by Ciarletta et al. [18], who proposed a hyperelastic theory of the layered structure of the intestine to reproduce its purely elastic passive response from the structural organization of its main constituents. The hyperelastic strain energy function is decoupled into an isotropic term, describing the ground biological matrix, and an anisotropic term, describing the single contributions of the directional fiber-reinforcements. Sokolis et al. [19-21] afforded comprehensive inflation/extension data of intestinal segments from distinct areas, spanning a physiologically relevant deformation range, and investigated in vitro the pseudo-elastic properties of tubular specimens from the ascending, mid, and descending colon, and the rectum of healthy Wistar rats under passive quasi-static conditions and a physiologic range of pressures/axial stretches. A neo-Hookean and five-fiber family model was chosen as a microstructure-based material model for its efficiency in producing accurate representations of the three-dimensional inflation/extension data in relation to the underlying microstructure. Although the above studies established many anisotropic hyperelastic constitutive models of human soft tissue, there is a lack of finite element models and analysis of human soft tissues, especially the intestine. The objective of this study is to develop a multi-layer finite element model of intestinal walls based on a hyperelastic theory of the layered structure of the intestine.

 

Constitutive Model

The intestinal wall was treated as a nonlinear, pseudo-elastic, homogeneous, and anisotropic material subjected to finite deformation [21]. An indicative scheme of the inner structure of the intestine walls includes the detection of four different layers consisting of mucous membrane,submucosa, longitudinal muscle and circular muscle layers. Two distinct fiber populations of collagen have been distinguished to run in a cross-ply arrangement, uniformly oriented at an angle over the longitudinal axis of the intestine [22].

 

HGO model

Holzapfel-Gasser-Ogden (HGO) model [7] regarded arteries be composed of thick-walled layers, each of them with a separate strain-energy function. From the engineering point of view, each layer may be considered as a composite reinforced by two families of fibers that are arranged in symmetrical spirals. Assume that each layer of arteries responds with similar mechanical characteristics. The kinematics of deformation are described locally in terms of the deformation gradient tensor, denoted as , relative to some reference configuration. The right Cauchy-Green tensor is defined by . Accordingly, the deformation gradient is decomposed multiplicatively as follows [10]:

(1)

where is the determinant of . Suppose that the material consists of anisotropic matrix material within which are embedded two families of fibres characterized by the two direction unit vectors . Define the following invariants with , and .

(2)

(3)

where are the isochoric counterparts of . Note that the invariants and are the squares of the stretches in the directions of and , respectively, so that they are stretch measures for the two families of fibers and therefore have a clear physical interpretation. The strain-energy function for arteries, , was split into two: a part associated with isotropic deformations and a part associated with anisotropic deformations [7].

(4)

where,

(5)

(6)

Here, is a stress-like material parameter, is a stress-like material parameter and is a dimensionless parameter. An appropriate choice of and enables the histologically based assumption that the collagen fibers do not influence the mechanical response of the artery in the low pressure domain to be modeled. The original HGO model that does not account for the dispersion is not able to capture accurately the stress-strain response of the whole layers. A invariant, , was introduced to characterize the dispersion of the collagen fibres of each family, and hence it controls the degree of anisotropy of the hyperelastic formulation, which certainly has a significant influence on the mechanical response. Then, in the HGO model (4) was modified by Gasser et al. [23] with the two transversely isotropic potentials , for the embedded families of collagen fibres, therefore, Eq.(4) was rewritten as the following Gasser-Ogden-Holzapfel (GOH) model.

(7)

where ,

(8)

Here, is a tensor invariant equal to the square of the stretch in the direction of , characterizes the distribution of the collagen fibres within the two families of fibres.

 

Hyperelastic constitutive model

The intestinal wall is considered as an anisotropic continuum with two directions of muscle-fiber reinforcement, represented by the unit longitudinal and circular vectors in the undeformed configuration, and a cross-ply collagen arrangement in the submucosa, in the directions described by the unit vectors and [18]. Here, define the structural tensors as,

(9)

The pseudo-invariants derived from the double contraction of the symmetric strain tensor and the structural tensors was expressed as,

(10)

Assume that the intestinal walls are incompressible materials. A decoupled expression of the strain energy function was used to describe the hyperelastic behavior.

(11)

where, is similar to that of Eq.(5), and,

(12)

 

Multi-Layer Finite Element Model

Assume that each layer of intestinal responds with similar mechanical characteristics. Since intestinal walls are composed of layers, it is desired to model each of these layers with a separate strain energy function instead of model (11). Eq.(12) can be rewritten with

(13)

In reference [23], the inflation of a thin-walled tube was investigated and a sketch of the thin-walled tube problem was provided, as shown in Fig. 1. It is assumed that the two families of collagen fibres are embedded symmetrically, with denoting the angle between the circumference and the mean orientation of the fibre families. Then, it is appropriate to model each layer of the intestinal wall as a fiber-reinforced composite.

(14)

where,

(15)

and are the principal stretches in the longitudinal and circumferential directions, respectively, and the mean direction of the fibres of each layer is given by the unit vector with components referred to the principal axes of the right Cauchy–Green tensor C. In equation (14), and represent the strain energy function for the longitudinal and circular muscle layer, respectively, and describes the reinforcement behavior of the collagen network in the submucosa. Here, is similar to that of Eq. (8).

 

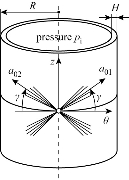
Fig. 1 Thin-wall approximation of the inflation of each layer with two embedded families of fibres. The mean orientations and the dispersion of the collagen fibres are characterized by and , respectively [23].

 

Results

The application of the proposed multi-layer finite element model requires a method for the characterization of intestinal tissue. The design of finite element methods involving all relevant deformations is necessary to obtain the best-fit values of the material constants of equation (14). In particular, uniaxial tensile tests performed on strip from the longitudinal and circumferential directions are considered. Since intestinal tissue is considered incompressible, planar biaxial testing allows for a two dimensional stress state that can be used to fully characterize its mechanical properties. Here, a narrow rectangular central part of referential length mm long, referential width mm and referential thickness mm, was considered as a specimen cut from the intestinal walls. The finite element computations used 500 eight-node composite brick elements shown as Fig. 2. The composite material of the brick element of the specimen consists of three layers, each of whom represents the longitudinal layer, circular layer and submucosa layer, respectively, as shown in Fig. 3. For hyperelastic constitutive model (11), an experimental procedure [18] has been proposed in order to characterize the passive response of porcine intestinal samples from planar uniaxial traction and shear tests. The fitted mechanical parameters, shown in Table 1, have been fitted in the least square sense with the results of the theoretical predictions. The principal stresses , from the uniaxial tensile tests in the longitudinal and circumferential directions, respectively, are given by

(16)

(17)

where,

(18)

and and are the principal stretches in the longitudinal and circumferential directions, respectively. Then, a finite element computation was used to investigate uniaxial strip tests related to multi-layer finite element model (14). For the numerical investigation, the material parameters were set to be similar to shown in Table 1. It remains to fit the remaining material parameters to the experimentally observed response of the intestinal layers. As mentioned, since the orientation of the collagen fibres among either the longitudinal or the circumferential layer is nearly isotropic, (i=a,b) of these two layers serves as a convenient initial measure for the fitting purpose. As with the findings in [23], the value of in the submucosa was chosen near to 0.226. Therefore, the investigations of potential (14) with respect to the structure parameters were carried out with the material parameters as given above, and, the angle of twist , varied within the ranges

(19)

Based on the results of numerical experiments, A set of appropriate parameters are collected in Table 2. Note that the cross-ply arrangement of collagen fiber in the submucosa has twisting angle . Fig. 4 and 5 show the computed Cauchy stress in the tensile direction in the longitudinal and circumferential specimens, where the outlines of the undeformed configurations, shown by solid lines, are superimposed. The curves of the experimental Cauchy stress under uniaxial traction, fitted with the predictions of the principal stresses given by Equations (16) and (17) in the longitudinal and circumferential directions, respectively, are depicted in Fig. 6 and 7. Furthermore, to verify the model，the intestine and a simplified capsule robot with legs were modelled as an axisymmetric structure, as shown in Fig. 8. The intestine was modelled as a hyperelastic deformable tube with the proposed constitute model and the capsule was modelled as a rigid body. As the boundary conditions for the analysis, both ends of the intestine were fixed in order not to rotate or move towards any directions. Fig. 9 shows the distribution of the equivalent Von Mises stress in the intestine after the complete deployment of capsule robot legs as computed by FEM simulations. It can be observed that stress concentration happens in the proximity of the contact regions between the capsule robot legs and the intestinal wall. The results demonstrate that the proposed constitutive model is able to describe the complex anisotropic behavior of intestinal tissue, showing the higher stiffening effect in the longitudinal direction.

 

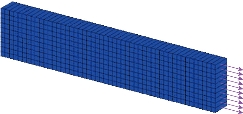
Fig. 2 A narrow rectangular central part considered as a specimen cut from intestinal walls.

 

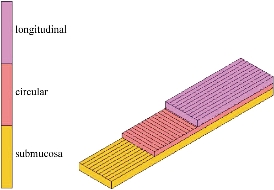
Fig. 3 Composition of each layer of composite material.

 

Table 1 Fitted value of the mechanical parameters of the hyperelastic model [18]

Mechanical parameters	c
Fitted value	1.58 KPa	2.17 KPa	0.84	77.12 KPa	0.516	22.01 KPa	12.1

 

 

 

 

Table 2 The material parameters () of the multi-layer model

Layer
longitudinal (=a)	0 KPa	0.3
circular (=b)	0.2 KPa	0.32
submucosa (=d)	1.58 KPa	0.25

 

 

 

 

 

 

 

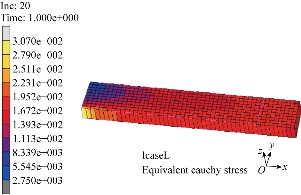
Fig. 4 Finite element computation of a uniaxial tension test in the longitudinal direction. The Cauchy stress in the direction of the applied load is plotted for a 4.0 N tensile load.

 

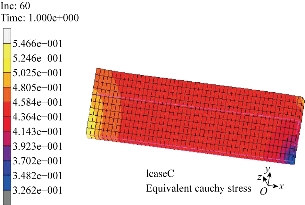
Fig. 5 Finite element computation of a uniaxial tension test in the circumferential directions. The Cauchy stress in the direction of the applied load is plotted for a 9.9 N tensile load.

 

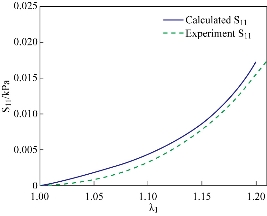
Fig. 6 Fitting of the uniaxial tensile test in the longitudinal direction.Solid line is numerical result calculated by Equation (16) while the dashed lines represents the experimental data in the longitudinal direction.

 

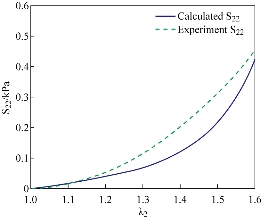
Fig. 7 Fitting of the uniaxial tensile test in the circumferential direction.Solid line is numerical result calculated by Equation (17) while the dashed lines represents the experimental data in the circumferential direction. 

 

Fig. 8 Schematic of the deployment of the capsule robot legs inside the intestine as implemented in the FEM simulations.

 

Fig. 9 Map showing a case of the distribution of the equivalent Von Mises stress in the intestine for the proposed model.

 

Conclusions

The present study provides a method to model the intestine walls as a fiber-reinforced composite which consists of two directions of muscle-fiber reinforcement and a cross-ply collagen arrangement. Based on an anisotropic hyperelastic theory of the layered structure, each layer was considered as a composite reinforced by two families of fibers, whose strain-energy function was described by GOH model. The proposed model was validated through finite element simulations by using the same form of strain-energy function for each layer, and the model parameters were optimized by fitting the model to the experimental stress-stretch responses in both longitudinal and circumferential directions.

 

Acknowledgements

This work was supported in part by the Project Sponsored by the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry, and in part by the Scientific Research Foundation for Young Teachers, Shanghai JiaoTong University.

 

Conflict of Interests

The authors declare that no competing interest exists.

 

References

1. C. Zhang, H. Liu, and H. Li, Experimental investigation of intestinal frictional resistance in the starting process of the capsule robot. Tribology International, 2014, 70: 11-17.
2. H.M. Kim, S. Yang, J. Kim, et al., Active locomotion of a paddling-based capsule endoscope in an in vitro and in vivo experiment (with videos). Gastrointestinal Endoscopy, 2010, 72(2): 381-387.
3. H. Zhou, A locomotion driving of the capsule robot in intestinal tract. International conference on intelligent robotics and applications. Springer International Publishing, 2014: 438-445.
4. J. Gao, G. Yan, Z. Wang, et al., A capsule robot powered by wireless power transmission: Design of its receiving coil. Sensors and Actuators A: Physical, 2015, 234(Supplement C): 133-142.
5. S.S. Mapara, V.B. Patravale, Medical capsule robots: A renaissance for diagnostics, drug delivery and surgical treatment. Journal of Controlled Release, 2017, 261 (Supplement C): 337-351.
6. W. El-Matary, Wireless capsule endoscopy: indications, limitations, and future challenges. Journal of Pediatric Gastroenterology & Nutrition, 2008, 46(1): 4-12.
7. G.A. Holzapfel, T.C. Gasser, and R.W. Ogden, A new constitutive framework for arterial wall mechanics and a comparative study of material models. Journal of Elasticity and the Physical Science of Solids, 2000, 61(1): 1-48.
8. G.A. Holzapfel, Determination of material models for arterial walls from uniaxial extension tests and histological structure. Journal of Theoretical Biology, 2006, 238(2): 290-302.
9. S. Federico, A. Grillo, G. Giaquinta, et al., Convex Fung-type potentials for biological tissues. Meccanica, 2008, 43(3): 279-288.
10. D.R. Nolan, A.L. Gower, M. Destrade, et al., A robust anisotropic hyperelastic formulation for the modelling of soft tissue. Journal of the Mechanical Behavior of Biomedical Materials, 2014, 39: 48-60.
11. Y. Zhu, G. Kang, and Q. Kan, et al., A finite viscoelastic–plastic model for describing the uniaxial ratchetting of soft biological tissues. Journal of Biomechanics, 2014, 47(5): 996-1003.
12. H. Khayyeri, A. Gustafsson, A. Heuijerjans, et al., A fibre-reinforced poroviscoelastic model accurately describes the biomechanical behaviour of the rat achilles tendon. PLOS ONE, 2015, 10(6): e0126869.
13. J.A. Peña, M.A. Martínez, and E. Peña, Layer-specific residual deformations and uniaxial and biaxial mechanical properties of thoracic porcine aorta. Journal of the Mechanical Behavior of Biomedical Materials, 2015, 50: 55-69.
14. Y. Zhu, G. Kang, C. Yu, et al., Logarithmic rate based elasto-viscoplastic cyclic constitutive model for soft biological tissues. Journal of the Mechanical Behavior of Biomedical Materials, 2016, 61: 397-409.
15. L.J. Sliker, G. Ciuti, M.E. Rentschler, et al., Frictional resistance model for tissue-capsule endoscope sliding contact in the gastrointestinal tract. Tribology International, 2016, 102: 472-484.
16. D.M. Pierce, T.E. Fastl, B. Rodriguezvila, et al., A method for incorporating three-dimensional residual stretches/stresses into patient-specific finite element simulations of arteries. Journal of the Mechanical Behavior of Biomedical Materials, 2015, 47: 147.
17. B. Fereidoonnezhad, R. Naghdabadi, S. Sohrabpour, et al., A mechanobiological model for damage-induced growth in arterial tissue with application to in-stent restenosis. Journal of the Mechanics and Physics of Solids, 2017, 101: 311-327.
18. P. Ciarletta, P. Dario, F. Tendick, et al., Hyperelastic model of anisotropic fiber reinforcements within intestinal walls for applications in medical robotics. The International Journal of Robotics Research, 2009, 28(10): 1279-1288.
19. D. Sokolis, I.K. Orfanidis, M. Peroulis, Biomechanical testing and material characterization for the rat large intestine: regional dependence of material parameters. Physiological Measurement, 2011, 32(12): 1969-1982.
20. D. Sokolis, S. Sassani, E. Kritharis, et al., Differential histomechanical response of carotid artery in relation to species and region: mathematical description accounting for elastin and collagen anisotropy. Medical & Biological Engineering & Computing, 2011, 49(8): 867-79.
21. D. Sokolis, S.G. Sassani, Microstructure-based constitutive modeling for the large intestine validated by histological observations. Journal of the Mechanical Behavior of Biomedical Materials, 2013, 21(3): 149-166.
22. Y. Zeng, A. Qiao, J. Yu, et al., Collagen fiber angle in the submucosa of small intestine and its application in gastroenterology. World Journal of Gastroenterology, 2003, 9(4): 804-807.
23. T.C. Gasser, R.W. Ogden, and G.A. Holzapfel, Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. Journal of The Royal Society Interface, 2006, 3(6): 15-35.

 

Copyright© Dasheng Liu, and Guozheng Yan, This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.