Stability of Anticancer Drug 5-Fluorouracil in Aqueous Solution: An Assessment of Kinetic Behavior - 2017-2018

Year
- 2023-2024
- 2021-2022
- 2019-2020
- 2017-2018
- 2015-2016
- 2013-2014
- 2011-2012
- 2009-2010
Catalogue

Home > Archives > Year > 2017-2018

←BACK

Research Article

Stability of Anticancer Drug 5-Fluorouracil in Aqueous Solution: An Assessment of Kinetic Behavior

Razzaq Abd Al-Zahra Ibrahim1*, Falah Shareef Abed Suhail2, Hussein Kadhem Al-Hakeim1

1 Department of Chemistry, Science Faculty, Kufa University, 54001 Najaf, Iraq.

2 Department of Pharmaceutical Chemistry, Pharmacy Faculty, Kufa University, 54001 Najaf, Iraq.

* Corresponding author. E-mail: razzaqalamery@gmail.com

Received: Mar. 22, 2018; Accepted: Jul. 6, 2018; Published: Aug. 10, 2018

Citation: Razzaq Abd Al-Zahra Ibrahim, Falah Shareef Abed Suhail, and Hussein Kadhem Al-Hakeim, Stability of Anticancer Drug 5-Fluorouracil in Aqueous Solution: An Assessment of Kinetic Behavior. Nano Biomed. Eng., 2018, 10(3): 224-234.

DOI: 10.5101/nbe.v10i3.p224-234.

Abstract

Spectroscopic measurements of pharmaceutical compound 5-fluorouracil (5-FU) drug was achieved in solvents with different polarity. The drug gave clear absorption peak at 259, 269, 270 and 266 nm in hexane, dimethyl sulfoxide (DMSO), N, N-dimethylformamide (DMF) and ethanol, as well as phosphate buffer respectively, which was consistent with the standard values in literatures. The results of extension coefficient (ε) and wave length (λmax) showed reduction in polar medium as compared to non-polar medium. The calibration curve of 5-FU drug was achieved by using serials solutions dissolved in phosphate buffer (pH=7.4 and T=37 oC) within the range of 1×10– 6 ~ 1×10– 4 M. The stability of 5-FU drug was studied in phosphate buffer at pH=5, 6, 7, 7.4 and 8 with 1×10– 5 M and T = 37 oC, according to the equation of first-order reaction. The hydrolysis of 5-FU disappeared at alkaline solution, but had noticeable hydrolysis in acidic solutions with the rate constant 25, 14 and 20 at pH of 5, 6 and 7 respectively. The calculation of molar extension coefficient and half-life (t1/2) showed same sequence of 5-FU hydrolysis. Then, rearrangement of obtained results offered complicated reversible equilibrium state by the combination between thermodynamic and kinetic behaviors of 5-FU hydrolysis; with Keq = 8.46, 6.11 and 142.8 at pH of 5, 6 and 7 respectively. The acidic hydrolysis of 5-FU occurred spontaneously within free energy (ΔG) did not exceed 10 kJ/mol, which meant the electro motive forces of interactions were weak, notable to release energy such as Van der Waals forces or hydrogen bonding.

Keywords: Stability of 5-FU; Physicochemical properties; Beer-Lambert relationship; Chemical affinity

Introduction

Cancer is one of the most dangerous diseases that are characterized by uncontrolled cellular growth (local tissue invasion) and distant metastasis (ability of invading surrounding tissues) [1]. Cancer leads to mortality, so it can be classified as the imperator of diseases according to American Cancer Society. There are four most common cancers are prostate, breast, lung and colorectal cancer [2].5-fluorouracil, i.e.5-fluoro-1H-pyrimidine-2,4-dione (5-FU) is phase specific drug that is a pyrimidine analog used in cancer treatment (Fig.1). It is an antineoplastic drug that interferes with nucleic acids growth by substituting it for the normal building blocks of RNA and DNA. This agent (trade names:Adrucil, Carac and Efudex) damages the cells during S phase (involved DNA replication in cell cycle of human body) for at least about 18 to 20 h. The anticancer drug (5-FU) was designed, synthesized and patented by Charles Heidelberger in 1957 [3, 4].One of the major mechanisms responsible for its antitumor activity is thymidylate synthesis by inhibition of DNA replication [5]. Some side effects of taking 5-FU might include diarrhea, nausea, vomiting, stomach/abdominal pain and general weakness [6]. Mostly, the drug is proceeded kinetically as a first-order reaction in aqueous solution and involved reversible equilibrium state. The system equilibrium consists of a forward reaction from reactants to products and an opposing back reaction from products to reactants. The rate of system equilibrium is equal to the summation of a forward and a backward rates [7, 8]. In this study, an assessment of the kinetic behavior stability of anticancer drug 5-FU at physiological conditions in aqueous solution was investigated.

Experimental

Materials

All chemicals used in the present investigation were obtained from commercial sources, with highest available purity. 5-FU was purchased from Sigma Aldrich, USA, with the purity of 99.99%. KH2PO4 and K2HPO4 of phosphate buffer solution (pH = 5 ~ 8) were obtained from Sdfine Chemical Limited-Mumbai, India. Hexane, ethanol, dimethyl formamide (DMF) and dimethyl sulfoxide (DMSO) were supplied by GCC-England with the purity of 99.99%.

Instruments and method

The electronic absorption spectra of ultraviolet-visible spectroscopy (UV-Vis) were recorded on Shimadzu (Japan) 1800PC-computrace spectrophotometer, version 2.42, 2016, by using 1cm matched quartz cells in aqueous solution of potassium phosphate buffer as a solvent. Measurements of pH were adjusted by using WTW (Germany) Inolap720 pH meter with electrode Sentix41. The distilled water produced by GFL (Germany) apparatus was purified via SG ionic exchangers. The prepared deionized water was measured in WTW (Germany) Inolap720 Conductivity meter. The temperature of prepared solutions was regulated within 37 oC, by using Julabo (Germany) circulator water bath. All weights were taken by a Mettler Toledo (Switzerland) SAB204S, sensitive electronic balance. All glassware was thoroughly cleaned with aqua region, and rinsed with distilled water as well as deionized water prior to use. The deionized water (conductivity = 0.5 ~ 0.7 µS/cm) was used to prepare all the solutions.

Preparation of buffer phosphate

Aqueous solutions of phosphate buffer were prepared by mixing a given volume of potassium dihydrogen phosphate (0.0666 M, 0.9063 gm in 100 mL) with dipotassium hydrogen phosphate (0.20 M, 3.4836 gm in 100 mL), and then its pH values was adjusted by using a pH meter [9, 10, 11].

Preparation of drug solutions

The solution of 5-FU drug (M.wt. = 130.08 gm/mol) was prepared with a concentration of 1×10– 3 M as a stock solution in different solvents by weight of 0.0130 gm in100 mL calibrated flask. Then, test solutions of 5-FU drug were prepared from the stock solution by a dilution process (the dilution must be less than 10 times) within the range of 1×10 – 6~ 1×10 – 4 M at T = 37 oC and pH = 7.4 of phosphate buffer.

Results and Discussion

Initially, 5-FU drug in aqueous solution showed clear peak at 266 nm, corresponding to a standard value [12, 13]. Then, the drug of 5-FU was measured with different polarities (Table 1) to determine the peak shifting of the analyte (Fig.1). Construction of the calibration curve for the analyte was achieved by using a series of solutions of 5-FU concentrations dissolved in the phosphate buffer. The range of 5-FU concentrations was 1×10 – 6 ~ 1×10 – 4 M, at physiological pH = 7.4 and T = 37 oC to simulate conditions of the human body. The prepared solutions of 5-FU drug were kept in circular water bath to obtain a thermal equilibrium during the period of experiment. Then, spectroscopic measurements of 5-FU solutions were taken directly in the same day of preparation and the obtained results are recorded in Table 2. The relationship between absorbance and the used concentrations (Beer-Lambert law) did not undergo deviation with high value of correlation coefficient (R2 = 0.9993, Y = 0.6624X + 0.0016) at λmax = 266 nm.The ideal linearity of absorbance and concentration for 5-FU drug was expressed in a limited range of 0.1×10 – 4 ~ 1×10 – 4 M especially (R² = 0.9988, Y = 0.6648X). It was found the ideal points for 5-FU drug in the aqueous solution of phosphate buffer at physiological pH = 7.4 and T = 37 oC (Fig. 2). The molar extinction coefficient had a relatively constant value, about ~7000 L/mol.cm for concentrations 0.04×10–4 ~ 1×10–4 M, which meant 5-FU molecules behaved as a single molecule (monomer) in aqueous solution without occurrence of any molecular aggregations at these conditions. Whereas, the high value of molar extinction coefficient at 0.02×10–4 M (ε = 9000 L/mol.cm) suggested that 5-FU molecules became independent (having free behavior) in diluted solution. The absorbance peak of 5-FU which appeared in ultraviolet region represented a π→π* transition, and was distinguished by a high value of molar extension coefficient [14, 15].

Table 1 Experimental results of 5-FU spectrums in various solvents at the same concentration and temperature (conc. = 1×10 – 4 M, T =37 oC)

Type of solvent	Hexane	Ethanol	DMF	DMSO	*H2O
Dielectric constant (ε0)	1.88	24.85	37.21	46.82	~ 78.35
λmax (nm)	259	266	270	269	266
Absorbance	0.110	1.328	1.549	1.089	0.673
ε (L/mol.cm)	1,100	13,280	15,490	10,890	6,730

Note: ε = extension coefficient; DMF = N, N-dimethylformamide; DMSO = dimethyl sulfoxide; *H2O =aqueous solution of phosphate buffer at pH = 7.4 (as a physiological condition).

Table 2 Concentration effect on absorbance of 5-FU in phosphate buffer at pH = 7.4, T = 37 oC and λ max = 266nm

Solution No.	1	2	3	4	5	6	7	8	9	10
Concentration (10‾ 4 M)	0.02	0.04	0.06	0.08	0.10	0.20	0.40	0.60	0.80	1.00
Absorbance	0.018	0.025	0.040	0.052	0.070	0.141	0.263	0.401	0.519	0.673
ε (L/mol.cm)	9000	6250	6666	6500	7000	7050	6575	6683	6487	6730

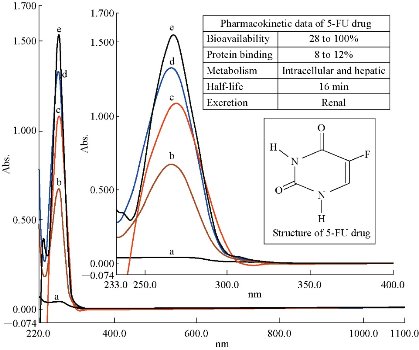
$D:\xwu\Nano Biomedicine and Engineering\Articles for production\排版\10(3)\(4) NBE-2018-0022\figs\raat1.jpg$

Fig. 1 5-FU spectra in some solvents at 1×10– 4 M: (a) Hexane; (b) *H2O; (c) DMSO; (d) Ethanol; and (e) DMF. (*H2O =aqueous solution of phosphate buffer at pH = 7.4 as a physiological condition; DMSO = dimethyl sulfoxide; DMF = N, N-dimethylformamide.)

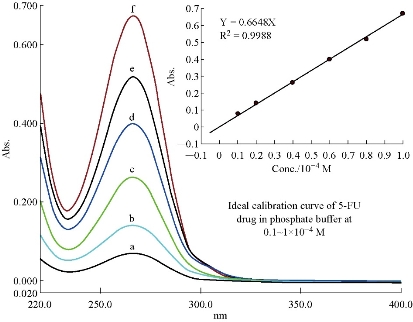
$D:\xwu\Nano Biomedicine and Engineering\Articles for production\排版\10(3)\(4) NBE-2018-0022\figs\raat2.jpg$

Fig. 2 Spectra of 5-FU at pH = 7.4, T = 37 oC, λmax = 266 nm: (a) 0.1×10 – 4 M; (b) 0.2 ×10 – 4 M; (c) 0.4×10 – 4 M; (d) 0.6×10 – 4 M; (e) 0.8×10 – 4 M; and (f) 1×10 – 4 M.

Stability of 5-FU drug at different acidic functions

The hydrolysis rate of 5-FU drug was studied in aqueous solution of phosphate buffer at different pH values as of 5.0, 6.0, 7.0, 7.4 and 8.0 (Table 4). The concentration of 5-FU drug was 1×10 – 5 M at T = 37 oC, which was prepared by dilution from 1×10– 4 M as prepared from fresh stock solution of 1×10– 3 M. The prepared solutions of drug were put in a circular water bath at T = 37 oC for 8~10 min to complete thermal homogeneity before beginning the first measurement. Maximum wave length of the drug shifted slightly, about λmax.= 266 nm at pH = 7.4, according to acidity function of the solution; and obtained results were recorded as following in Table 3. The results of drug hydrolysis at different pH (Table 3) show that 5-FU did not undergo noticeable hydrolysis in alkaline solutions at pH = 7.4 and 8.0. This was supported by tiny changes of absorbance with time (At), in addition to the return of absorbance into the same value at initial time (absorbance at 1440 min was equal to absorbance at 10 min). Therefore, the hydrolysis rate of 5-FU drug at pH = 5.0, 6.0 and 7.0 could be calculated according to the equation of first-order reaction (Eq. 1) by plotting ln(At) versus time (slope= k*) [8] as follows.

ln(At) = ln(Ao) – k* t, (1)

where Ao refers to primary absorbance of drug at origin time. The change in hydrolysis rate constant of 5-FU drug at pH = 6.0 and 5.0 was relatively constant (Δk/ΔpH = 0.0011 /min), while the difference between pH = 6.0 and 7.0 was smaller than previous value by five times (Δk /ΔpH = 0.0006 /min). The hydrolysis rate (k*) and absorbance with time (At) at pH= 7.0 was higher than that with the same parameters at pH = 6.0 (Table 3, 4 and Fig. 3). To explain this phenomenon, a pervious result at different pH was repeated again for three times; but without any changes in absorbance values at limited pH. Then, the molar extinction coefficient ε that represented real absorbance value of 5-FU hydrolysis could be calculated at different pH (Table 5) by Beer-Lambert law [8, 14]. The absorbance of 5-FU drug before hydrolysis, [5-FU]o ≡ Ao, was extracted from the intercept point of straight line which was plotted for absorbance with time, At (Table 3), at different pH and T = 37 oC (Fig. 4). The real absorbance value ε has great importance, since it represents the photons that cause excitation of electrons from highest occupied molecular orbital (HOMO) to lowest unoccupied molecular orbital (LUMO) (5-FU + light → 5-FU*) [8]. The obtained results of extinction coefficient decreased as a function to pH in alkaline direction. But this decreasing in extinction coefficient at pH = 6.0 was the minimum in comparison with the others at pH = 5.0 ~7.0. This dissimilarity in the decreasing of extinction coefficient at different pH led to computation of the parameter ε with time. As well as, the calculation of half-life (t1/2 = 0.693 / k*) of 5-FU hydrolysis at different pH (Table 6) according to the equation of first-order reaction [16]. The experimental data as shown in Table 6 can be arranged in suitable diagram by plotting molar extinction coefficient versus pH to make them more clarity (Fig. 5).Then, a similar diagram was plotted of k* (/min) versus pH according to results in Table 4. From the obtained experimental results of 5-FU hydrolysis at different pH (Table 5, 6, Fig. 3 and 5), some conclusions could be summarized as follows: The chemotherapy compound 5-FU was hydrolyze in acidic media at pH = 5.0, depending on the values of Ao, εo and k* of 5-FU the highest. In addition, the half-life of 5-FU at pH = 5.0 (t1/2 = 277.20 min.) had a lower value in comparison with those at pH = 6.0 and 7.0, which meant that the hydrolysis did not need long time. This interpreted the cause of high physicochemical properties, i.e. ε o and k*, in acidic media at pH = 5.0. The hydrolysis behavior of 5-FU had been modified in a neutral medium at pH = 7. Because the absorbance at infinite A∞ = 0.1000 and ε1440 = 10,000 L/(mol.cm) was equal to the value at initial Ao= 0.1007 and εo= 10,070 L/(mol.cm), and half-life t1/2 = 346.50 min. In addition, the behavior of 5-FU drug at pH = 7.0 could be supported by the slight hydrolysis (undetermined) in alkaline media at pH = 7.4 and 8.0 respectively. Yet, the behavior of 5-FU drug in the aqueous solutions was expected in acidic and alkaline media, since it is constantly described in literatures as analog derivatives into a pyrimidine base (nitrogen base) [17, 18, 19]. But the problem occurred at pH = 6.0 when absorbance decreased with time, essentially at A∞= 0.082 and molar extinction coefficient ε∞ = 8,200 L/(mol.cm). This fact led to decrease in the rate constant of 5-FU hydrolysis k*= 14×10– 4 /min, and increase in half-life of hydrolysis t1/2* = 495.0 min. Mostly, 5-FU hydrolysis at pH = 6.0 might be due to the partial dissociation, as seen in the dissociation of amino acids at different acidity, with a net charge = 0.0 as a Zwitter ion (Eq. 3). This meant that 5-FU drug in acidic media (pH = 5.0) had net charge = partial negative charge (Eq. 2), while in alkaline media (pH = 7.0) it had a partial positive charge (Eq. 4). So, the hydrolysis processes of 5-FU drug at different pH could be explained depending on these assumptions as follows:

In pH = 5.0: 5-FU + nH + (5-FU) ---- (H+)n, (2)

in pH = 6.0: 5-FU + nH + (5-FU) ---- (H+)n, (3) and

in pH = 7.0: 5-FU + nH + (5-FU) ---- (H+)n, (4)

where n refers to number of ions, and H+ means hydrogen ions. Therefore, hydrolysis of 5-FU drug proceeded in forward direction at pH=7.0 as a simple process. But it showed simple equilibrium state at pH = 5.0, and relaxation state led to the decrease of all physical properties at pH=6.0 in comparison to the other conditions. It suggested that 5-FU drug hydrolyzed in aqueous solutions of phosphate buffer as a complicated process from first-order reaction, instead of as a simple hydrolysis as assumed previously. It required rearrangement of the same data for 5-FU hydrolysis at different pH (Table 3) as a reversible equilibrium reaction.

Table 3 Time effect on absorbance of 5-FU (1×10–5M) in phosphate buffer at pH = 5.0 ~ 8.0 and T = 37 oC

pH of solution		5.0		6.0		7.0		7.4	8.0
λmax of 5-FU (nm)		265.0		265.5		266.0		266.0	267.2
Abs. with time ≡ At		At	ln(At)	At	ln(At)	At	ln(At)	At	At
Time of measurement (min)	10	0.139	– 1.9732	0.094	– 2.3644	0.099	– 2.3126	0.073	0.061
	20	0.136	– 1.9951	0.093	– 2.3751	0.097	– 2.3330	0.073	0.059
	30	0.132	– 2.0249	0.092	– 2.3859	0.095	– 2.3538	0.075	0.059
	40	0.129	– 2.0479	0.090	– 2.4079	0.093	– 2.3751	0.075	0.059
	50	0.125	– 2.0794	0.089	– 2.4191	0.091	– 2.3968	0.080	0.059
	60	0.123	– 2.0955	0.088	– 2.4304	0.090	– 2.4079	0.080	0.059
	70	0.123	– 2.0955	0.088	– 2.4304	0.090	– 2.4079	0.080	0.059
	80	0.123	– 2.0955	0.088	– 2.4304	0.090	– 2.4079	0.080	0.059
	90	0.123	– 2.0955	0.088	– 2.4304	0.090	– 2.4079	0.080	0.059
	100	0.123	– 2.0955	0.088	– 2.4304	0.090	– 2.4079	0.080	0.060
	110	0.123	– 2.0955	0.088	– 2.4304	0.090	– 2.4079	0.080	0.060
	120	0.123	– 2.0955	0.088	– 2.4304	0.090	– 2.4079	0.080	0.060
	1440	0.127	– 2.0635	0.082	– 2.5010	0.100	– 2.3025	0.073	0.061

Note: λmax = maximum wave length; Abs. = absorbance; ln(At) = ln(absorbance) versus time.

Table 4 The hydrolysis rate constant of 5-FU drug (1×10–5 M) in aqueous solution of potassium phosphate buffer at pH = 5.0, 6.0 and 7.0 with T = 37 oC, according to equation of first-order reaction

pH of solution	Straight line equation (Eq.1) of 5-FU hydrolysis.	Correlation factor ( R2 )	Slope = –k* (/min)	Apparent forward rate constant (k*)
pH of solution	( Y = a X + b )	Correlation factor ( R2 )	Slope = –k* (/min)	k* (/min ×10 – 4)
5.0	Y = – 0.0025X – 1.9473	0.9951	– 0.0025	25.00
6.0	Y = – 0.0014X – 2.3487	0.9877	– 0.0014	14.00
7.0	Y = – 0.0020X – 2.2943	0.9936	– 0.0020	20.00
7.4	No change in At (stable)	--	--	--
8.0	No change in At (stable)	--	--	--

Note: X = ln(At); Y = time of measurement (min); a = slope (– k*); b = ln(Ao).

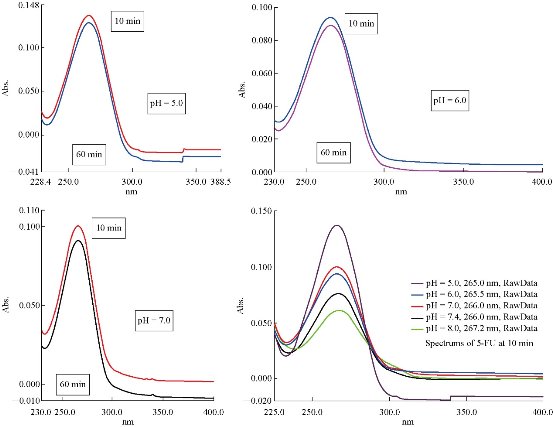
$D:\xwu\Nano Biomedicine and Engineering\Articles for production\排版\10(3)\(4) NBE-2018-0022\figs\raat3.jpg$

Fig. 3 Spectra of 5-FU hydrolysis with 1×10– 5 M in phosphate buffer at different pH and T= 37 oC.

Table 5 Molar extinction coefficient of 5-FU (1×10 – 5 M) in phosphate buffer at different pH and T = 37 oC

pH of solution	Straight line equation for absorbance vs. time of 5-FU	Correlation factor ( R2 )	(A)o ≡ [5FU]o	Molar extinction coefficient
pH of solution	Y = a X + b	Correlation factor ( R2 )	(A)o ≡ [5FU]o	εo (L/mol.cm)
5.0	Y = – 0.0003X + 0.142	0.9943	0.142	14,200
6.0	Y = – 0.0001X + 0.0954	0.9878	0.0954	9,540
7.0	Y = – 0.0002X + 0.1007	0.9922	0.1007	10,070
7.4	No change in A t (stable)	--	0.0730	7,300
8.0	No change in A t (stable)	--	0.0610	6,100

Note: (A)o ≡ [5FU]o refers to absorbance of 5-FU before hydrolysis at origin time.

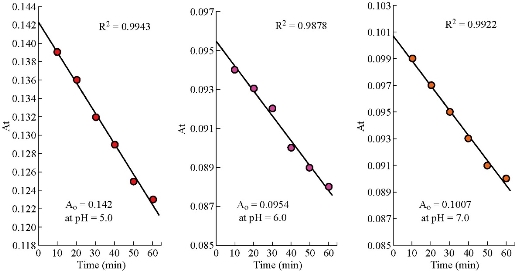
$D:\xwu\Nano Biomedicine and Engineering\Articles for production\排版\10(3)\(4) NBE-2018-0022\figs\raat4.jpg$

Fig. 4 The diagram of absorbance of 5-FU drug (1×10–5 M) before hydrolysis ([5FU]o ≡ Ao) in potassium phosphate buffer at different pH and T=37 oC, where Y axis = At, X axis = time (min).

Table 6 Molar extinction coefficient with half-life of 5-FU (1×10 –5 M) at different pH and 37 oC.

pH of solution	Absorbance of 5-FU with time		Molar extinction coefficient εt (L/mol.cm)		Apparent half-life of 5-FU hydrolysis
pH of solution	10 min.	1440 min.	ε10	ε1440	t1/2* (min)
5.0	0.139	0.127	13,900	12,700	277.20
6.0	0.094	0.082	9,400	8,200	495.00
7.0	0.099	0.100	9,900	10,000	346.50
7.4	0.073	0.073	7,300	7,300	--
8.0	0.061	0.061	6,100	6,100	--

Note: t1/2* refers to apparent half-life of 5-FU hydrolysis.

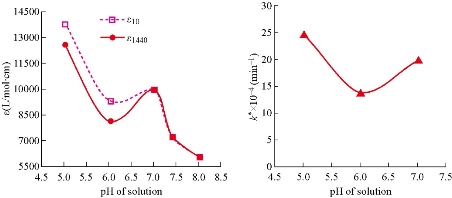
$D:\xwu\Nano Biomedicine and Engineering\Articles for production\排版\10(3)\(4) NBE-2018-0022\figs\raat5.jpg$

Fig. 5 The molar extinction coefficient εt and rate constant k* of 5-FU hydrolysis with concentration as of 1×10 – 5 M in aqueous solution of phosphate buffer at different pH and 37 oC.

Stability of 5-FU hydrolysis as a reversible first-order reaction

The assumptions (Eq. 2, Eq. 3 and Eq. 4) might involve equilibrium state in some cases, which meant a hydrolysis of 5-FU drug was a reversible complex process of first-order reaction. So, the hydrolysis product, Ax ≡ x, of 5-FU in aqueous solution could be calculated by depending on the values of At ≡ a－x (Table 3) as subtracted from Ao ≡ a (Table 5). Then, the obtained results could be applied in the equation of reversible equilibrium reaction from first-order reaction (Eq. 5) of 5-FU drug at different pH (Table 7). Also, the equilibrium constant Keq of 5-FU hydrolysis could be calculated at different pH as a thermodynamic behavior according to Eq. 6 [7, 8] (Table 8).

ln(Ae /Ae – Ax) = (k1 + k –1)t, (5) and

Keq = Ae / Ao – Ae. (6)

Ae: absorbance of 5-FU at equilibrium (1440 min); Ax: absorbance of 5-FU produced with time; k1: forward rate constant; k –1: backward rate constant; t: time of measurement (min); and Ao: primary absorbance of 5-FU drug before hydrolysis at origin time. Mathematically, the plotting of ln(Ae / Ae – Ax) versus time must produce straight line with slope equal to k1 +k –1 (/min), which represents the kinetic behavior of 5-FU hydrolysis at different pH, as shown in Fig.6. In addition, the thermodynamic and kinetic behaviors could be combined (Eq. 5 and 6) to calculate the rate constants k1 and k –1, respectively, of 5-FU hydrolysis in phosphate buffer solution at different pH according to equation of reversible first-order reaction (Table 8). The new results of hydrolysis of 5-FU drug at different pH were acceptable and more useful at pH = 6.0 especially, as a result of the high linearity of straight line and the large approximation between simple and complicated hydrolysis of 5-FU drug in aqueous solution of phosphate buffer at different pH and T = 37 oC (Table 4 and 8). The equilibrium constant values (as a measurement of stability in Table 8) of 5-FU hydrolysis at different pH ensured the acceptability of assumptions 2, 3 and 4. So, the half-life (t1/2)total of equilibrium 5-FU hydrolysis could be determined exactly: (t1/2)total = 0.693 / k1 + k –1[16], where Ax = 0.5Ae (Eq. 5). Then, by assuming that the hydrolysis of 5-FU drug was first-order reaction in both directions, the forward half-life (t1/2)f = 0.693 / k1 and the backward half-life (t1/2)b = 0.693 / k –1 could be extracted, respectively (Table 9) [17]. After all these calculations, the apparent rate constant k* and half-life of 5-FU hydrolysis (Table 4 and 6) as a simple process from first-order reaction, with similarities represented by the physical parameters in reversible equilibrium hydrolysis (Table 8 and 9) could be assessed as follows: At pH = 7.0, no difference in the half-life t1/2*= (t1/2)total = 346.5 min and (t1/2)f = 348.92 min which was much lower than (t1/2)b=49848.94 min. In addition, k*= 20×10– 4 ≈ k1= 19.86×10– 4 /min, and the highest stability constant Keq= 142.85. All these values led to hydrolysis of 5-FU drug at pH = 7.0 proceeding in forward direction of first-order reaction without any complications. Otherwise, the hidden likelihood might exist that a limited quantity of 5-FU drug was hydrolyzed at exact time without other unidentified processes in the neutral solution, leading to an increase in absorbance, rate constant and stability. At pH = 5.0, there was simple equilibrium state of 5-FU drug, because a difference in half-life t1/2* – (t1/2)total = 277.20 min – 256.66 min = 20.54 min, and it had (t1/2)b = 2424.26 min, which was considered a lower value in comparison with the others. However, the hydrolysis process was more motive towards forward than towards backward direction, since k1 = 24.14×10–4 /min, higher than k –1 = 2.85×10– 4 /min, and (t1/2)f = 287.05 min, even higher than t1/2*. In addition, the equilibrium constant Keq = 8.46666 was expected satisfactorily in comparison with others. At pH = 6.0, in spite of the high close values between k*= 14×10– 4 ≅ k1 = 13.75×10 – 4 /min, and (t1/2)f – t1/2* = 503.90 min – 495 min = 8.90 min, there was a high variation between t1/2* – (t1/2)total = 495 min – 433.12 min= 61.875 min, which might be due to a relaxation time of the equilibrium state [8]. Also, values of (t1/2)b = 3083.60 min and Keq = 6.11940 possibly contributed to creating the complicated equilibrium state. This probability might explain the decreasing in absorbance, rate constant of hydrolysis and stability of 5-FU at pH = 6.0 in comparison with those at pH = 7.0.

Table 7 Time effect on absorbance of 5-FU (1×10– 5 M) in aqueous solution of phosphate buffer at pH = 5.0 ~ 7.0 and T = 37 oC, as reversible equilibrium reaction from first-order reaction.

Hydrolysis of 5-FU drug at pH = 5.0 and λmax = 265 nm as a reversible first-order reaction
Time (min)	At	Ao	Ax ≡ x		Ae / Ae – Ax		ln(Ae / Ae – Ax)
10	0.139	0.142	0.003		1.02419		0.023905
20	0.136	0.142	0.006		1.04958		0.048396
30	0.132	0.142	0.010		1.08547		0.082013
40	0.129	0.142	0.013		1.11403		0.107988
50	0.125	0.142	0.017		1.15454		0.143706
60	0.123	0.142	0.019		1.17592		0.162055
Equilibrium	0.127	0.142	0.015		1.13392		0.125688
Hydrolysis of 5-FU drug at pH= 6.0 and λmax = 265.5 nm as a reversible first-order reaction
Time (min)	At	Ao	Ax ≡ x	Ae / Ae – Ax		ln(Ae / Ae – Ax)
10	0.094	0.0954	0.0014	1.017369		0.017220
20	0.093	0.0954	0.0024	1.030150		0.029705
30	0.092	0.0954	0.0034	1.043256		0.042347
40	0.090	0.0954	0.0054	1.070496		0.068122
50	0.089	0.0954	0.0064	1.084656		0.081262
60	0.088	0.0954	0.0074	1.099195		0.094578
Equilibrium	0.082	0.0954	0.0134	1.195335		0.178426
Hydrolysis of 5-FU drug at pH = 7.0 and λmax = 266 nm as a reversible first-order reaction
Time (min)	At	Ao	Ax ≡ x	Ae / Ae – Ax		ln(Ae / Ae – Ax)
10	0.099	0.1007	0.0017	1.017293		0.017146
20	0.097	0.1007	0.0037	1.038421		0.037701
30	0.095	0.1007	0.0057	1.060445		0.058688
40	0.093	0.1007	0.0077	1.083423		0.080126
50	0.091	0.1007	0.0097	1.107419		0.102032
60	0.090	0.1007	0.0107	1.119820		0.113168
Equilibrium	0.100	0.1007	0.0007	1.007049		0.007024

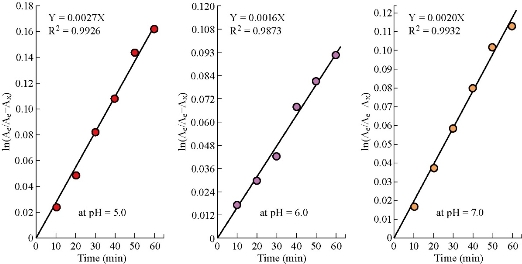
$D:\xwu\Nano Biomedicine and Engineering\Articles for production\排版\10(3)\(4) NBE-2018-0022\figs\raat6.jpg$

Fig.6 Diagrams show the rates of reversible equilibrium hydrolysis of 5-FU drug (1×10–5 M) in aqueous solution of potassium phosphate buffer at different pH and T = 37 oC.

Table 8 Thermodynamic and kinetic parameters of 5-FU drug (1×10–5 M) as reversible equilibrium hydrolysis in aqueous solution of phosphate buffer at different pH at T = 37 oC

pH of solution	Y = a X	R2	k1×10– 4 (/min)	k –1× 10– 4 (/min)	Keq
5.0	Y = 0.0027X	0.9926	24.1414	2.8586	8.46666
6.0	Y = 0.0016X	0.9873	13.75262	2.24737	6.11940
7.0	Y = 0.0020X	0.9932	19.86097	0.13902	142.8571
7.4	Stable	--	--	--	--
8.0	Stable	--	--	--	--

Table 9 Half-life of 5-FU drug (1×10– 5 M) in aqueous solution of phosphate buffer at different pH and T = 37 oC, as a reversible equilibrium hydrolysis from first-order reaction

pH of solution	Equilibrium of 5-FU (t1/2)total (min)	Forward hydrolysis of 5-FU (t1/2)f (min)	Backward hydrolysis of 5-FU (t1/2)b (min)
5.0	256.666	287.058	2424.263
6.0	433.125	503.903	3083.604
7.0	346.500	348.925	49848.9426

Free energy and chemical affinity of 5-FU hydrolysis

The free energy expresses the progress of chemical reaction (direction) and describes the reactants and products at equilibrium state. The standard free energy ΔGo represents useful physical property in biochemical processes, and can be determined in stoichiometry depending on Gibbs free energy equation (Eq. 7):

ΔGo = − RT ln Keq, (7)

where R is gas constant (8.314 J/K.mol), and T is the absolute temperature (310 oK). Then, the chemical affinity Ah, as a Helmholtz constant, representing motive force of molecules in reaction to constant temperature could be extracted from Eq. 8. It had the same value of standard free energy but differed in sign, which means Ah = positive (+ve) of spontaneous processes (ΔGo = –ve) and vice versa.

Ah= – (ΔGo)T, P, n, (8)

where T is temperature, p is pressure, and n is mole number. Therefore, the values of ΔGo and Ah of 5-FU hydrolysis in aqueous solution of phosphate buffer at different pH could be calculated (Table 10) depending on the equilibrium constant (Table 8) [18]. In general, there are some important principles that must be presented essentially for a system at equilibrium state: The equilibrium constant is considered as a ratio of reaction rate constants k1 / k–1, or relative amount of reactants into products, but not as the reaction rates. Equilibrium represents dynamic state, even at absence of the net change in reactants or products concentration, because the individual molecules of reactants or products would be in the state of inter conversion continually [19]. The numeric value of equilibrium constant Keq is not affected by the pressure, the concentration variation and the volume which changes the equilibrium position only. But the equilibrium constant would be changed at different temperatures, thus must be constant and recoded at measurement [18]. Therefore, the difference of pH of solution cannot change the value of equilibrium constant of 5-FU hydrolysis (Table 10), since ) act as a catalyst of this process. Usually, catalyst can accelerate the rate of reaction by lowering the activation energy as a result of changing the mechanism of reaction. Therefore, 5-FU at pH = 6.0 may undergo many transient modifications during the catalysis process, which was the major reason that made hydrolysis a complicated process, and decreasing Keq, ΔG o and Ah values. The notable fact from the difference in 5-FU hydrolysis (represented by physical parameters) due to the type of interactions that occurred in the solute of 5-FU drug at limited pH. Since these interactions (possibly as a Van der Waals forces) were responsible for increasing the rate of 5-FU hydrolysis at pH = 5.0 and 7.0 in forward direction (k1). Consequently, the state functions Keq, ΔGo and Ah (depending on the initial and final states of reacting species) had high values to explain the progress and affinity periods of hydrolysis [20-22].

Table 10 Thermodynamic parameters of 5-FU drug (1×10–5 M) in aqueous solution of phosphate buffer at different pH and T = 37 oC as a reversible equilibrium hydrolysis

pH of solution	Thermodynamic parameters: Equilibrium constant Keq, Free energy change ΔG o and chemical affinity Ah
pH of solution	Keq	ln Keq	ΔG o (J/mol)	Ah (J/mol)
5.0	8.46666	2.13613	– 5508.21298	5508.21298
6.0	6.11940	1.81146	– 4671.01909	4671.01909
7.0	142.8571	4.96184	– 12794.54984	12794.54984
7.4	Stable	--	--	--
8.0	Stable	--	--	--

Conclusions

Analytically, the suitable concentrations of 5-FU drug showed a linear relationship of Beer-Lambert law at 1×10–6 ~ 1×10–4 M, pH = 7.4 and T = 37 oC. The drug of 5-FU did not undergo noticeable hydrolysis in alkaline solutions, but it showed hydrolysis rate as first-order reaction (k*) in acidic media. The calculated molar extension coefficient and half-life (t1/2) showed the same sequence of 5-FU hydrolysis, and the hydrolysis at pH=6.0 appeared as a partial dissociation (Zwitter ion). Rearrangement of the same results proved that 5-FU hydrolysis had complicated reversible equilibrium state that occurred spontaneously by Van der Waals interactions or by hydrogen bonding.

Conflict of Interests

The authors declare that no competing interest exists

References1.

B.A. Chabner, D.L. Longo, Cancer chemotherapy and biotherapy principles and practice, 4th.ed. Lippincott Williams and Wilkins Press, 2006: 285.
A. Jemal, R. Siegel, and E. Ward, Cancer statistics, American cancer society study. CA Cancer J. Clin., 2007, 17: 291-293.
American Cancer Society, Chemotherapy principles: An in-depth discussion of the techniques and its role in cancer treatment. American Cancer Society, 2013: 120-129.
American Cancer Society, Communicating cancer information through mass distribution leaflets — an american cancer society study. CA Cancer J. Clin., 1967, 17: 291-293.
K. Hartmann, C. Heidelberger, Studies on fluorinated pyrimidines: Inhibition of thymidylate synthetase. J. Biol. Chem., 1961, 236:3006.
M.B. Mohamed, N.T. Adbel-Ghani, O.M. El-Borady, et al., 5-Fluorouracil Induces Plasmonic Coupling in Gold Nanospheres: New Generation of Chemotherapeutic Agents. J. of Nanomedicine and Nanotechnology, 2012, 3: 146.
A.G. Whittaker, A.R. Mount, and M.R. Heal, Physical chemistry. BIOS Scientific Ltd., 2005: 184-186.
P. Monk, Physical Chemistry: Understanding our chemical world. John Wiley and Sons Ltd., 2004: 385-460.
A.I. Vogel, Quantitative in organic analysis, 3rd ed. Longman Group Limited, 1964: 156-243.
D.D. Perrin, B.B. Dempsy, Buffers for PH and metal ion control. John Wiley and Sons, 1974: 50-86.
P.L. Williams, R.C. James, and S.M. Roberts, Principles of toxicology: Environmental and industrial application, 2nd. ed. John Wiley and Sons, 2000: 341.
N. Zhang, Y. Yin, and S.J. Xu, 5-Fluorouracil: Mechanisms of resistance and reversal strategies. J. of Molecules, 2008, 13(8): 1551-1569.
J.E.F. Reynolds, Martindale: The extra pharmacopoeia, 31st ed. Royal Pharmaceutical Society, 1996: 572-575.
P. Atkins, J. de Paula, Physical chemistry, 8th.ed. Oxford University Press, 2010: 638-1095.
I. Bak, Modern analytical techniques in the pharmaceutical and bioanalysis. Szechenyi Terv, 2011: 74-80.
P. Atkins, L. Jones, Chemical principles: The quest for insight, 1st ed. W. H. Freeman Company, 1999: 606-631.
R. Aydin, M. Pulat, 5-Fluorouracil encapsulated chitosan nanoparticles for pH - stimulated drug delivery: Evaluation of controlled release kinetics. J. of Nanomaterials, 2012: 1-10.
W.J. Moore, Physical chemistry, 5th.ed. Longman Group Ltd., 1972: 339-340.
K. Murray, K. Granner, A. Mayes, et al., Harper’s illustrated biochemistry, 26th ed. Mc Graw-Hill Companies, 2003: 92-288.
M.L. Laghnbal, Fundamentals of thermodynamics. John Wiely and Sons, 1989: 210.
J.W. Tester, M. Modell, Thermodynamics and its applications, 3rd.ed. Prentic Hall PTR, 1997: 385.
O.A. Hatem, F. Suhail, and A.M. Juda, Determination of chemical potential for carvedilol, atenolol and Propranolol diffusion through SDS micelle solution. J. Der. Pharma. Chemica, 2016, 8(5): 276-286.

Copyright© Razzaq Abd Al-Zahra Ibrahim, Falah Shareef Abed Suhail, and Hussein Kadhem Al-Hakeim. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.